TRIGONOMETRIC RATIOS EXAMPLES AND SOLUTIONS

Example 1 :

Compare the sine, the cosine, and the tangent ratios for ∠A in each triangle below.

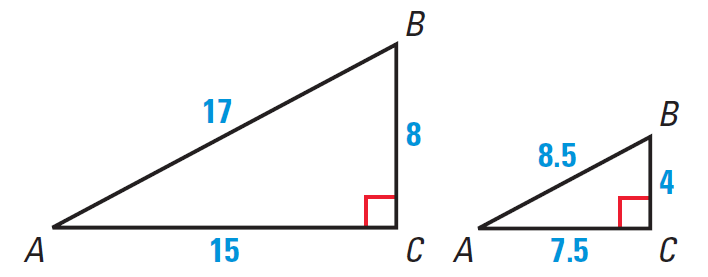
Solution :

By the SSS Similarity Theorem, the triangles are similar. Their corresponding sides are in proportion, which implies that the trigonometric ratios for ∠A in each triangle are the same.

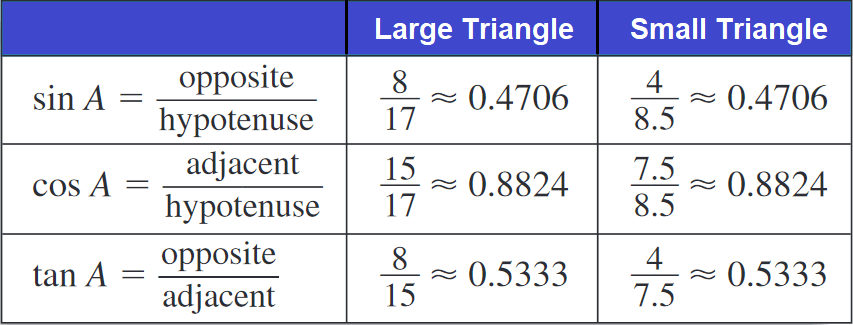
Trigonometric ratios are frequently expressed as decimal approximations.

Example 2 :

Find the sine, the cosine, and the tangent of the indicated angle.

a.  ∠S          b.  ∠R

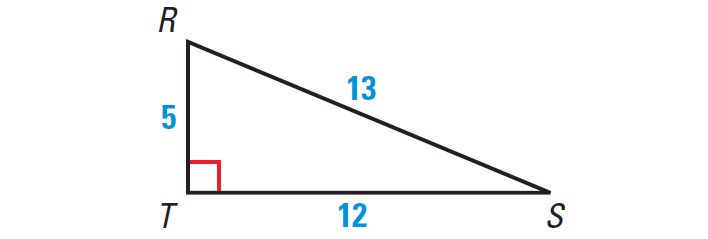
Solution (a) :

The length of the hypotenuse is 13. For ∠S, the length of the opposite side is 5, and the length of the adjacent side is 12.

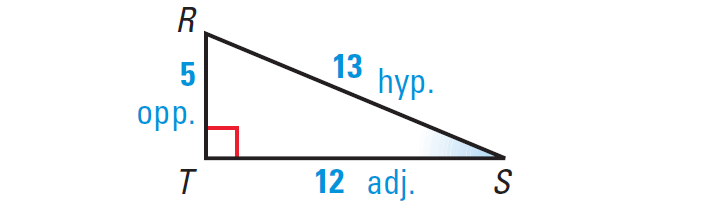
sin S  =  opp./hyp.  =  5/13  ≈  0.3846

cos S  =  adj./hyp.  =  12/13  ≈  0.9231

tan S  =  opp./adj.  =  5/12  ≈  0.4167

Solution (b) :

The length of the hypotenuse is 13. For ∠R, the length of the opposite side is 12, and the length of the adjacent side is 5.

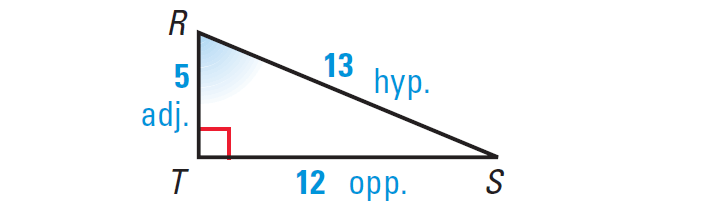
sin R  =  opp./hyp.  =  12/13  ≈  0.9231

cos R  =  adj./hyp.  =  5/13  ≈  0.3846

tan R  =  opp./adj.  =  12/5  ≈  2.4

Example 3 :

Find the sine, the cosine, and the tangent of 45°. 

Solution :

Begin by sketching a 45°-45°-90° triangle. Because all such triangles are similar, we can make calculations simple by choosing 1 as the length of each leg. From the Pythagorean Theorem, it follows that the length of the hypotenuse is √2.

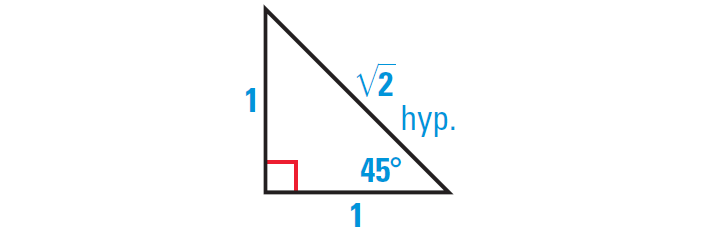
sin 45°  =  opp./hyp.  =  1/√2  =  √2/2  ≈  0.7071

cos 45°  =  adj./hyp.  =  1/√2  =  √2/2  ≈  0.7071

tan 45°  =  opp./adj.  =  1/1  =  1

Example 4 :

Find the sine, the cosine, and the tangent of 30°. 

Solution :

Begin by sketching a 30°-60°-90° triangle. To make the calculations simple, we can choose 1 as the length of the shorter leg. From 30°-60°-90° Triangle theorem,  it follows that the length of the longer leg is √3 and the hypotenuse is 2.

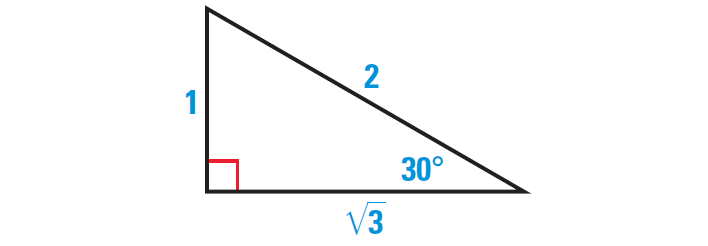
sin 30°  =  opp./hyp.  =  1/2  =  0.5

cos 30°  =  adj./hyp.  =  √3/2  ≈  0.8660  

tan 30°  =  opp./adj.  =  1/√3  =  √3/3  ≈  0.5774

Example 5 :

Jacob is measuring the height of a Sitka spruce tree in North Carolina. He stands 45 feet from the base of the tree. He measures the angle of elevation from a point on the ground to the top of the tree to be 59°. How can he estimate the height of the tree ? 

Solution :

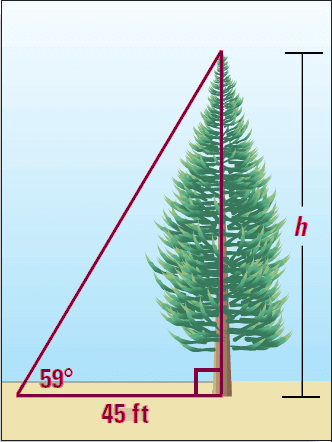
To estimate the height of the tree, Jacob can write a trigonometric ratio that involves the height h and the known length of 45 feet.

In the above right triangle, for the angle 59°, h is opposite side and the side has length 45 ft is adjacent side. 

The trigonometric ratio that involves opposite side and adjacent side is tangent. 

Write ratio : 

tan 59°  =  opp./adj. 

Substitute. 

tan 59°  =  h/45

Multiply each side by 45. 

45 ⋅ tan 59°  =  h

Use calculator or table to find the value of tan 59° and substitute. 

45 ⋅ 1.6643  =  h

Simplify.

74.9  ≈  h

So, the tree is about 75 feet tall. 

Example 6 :

The escalator at the University Metro Rail Station near University of Miami in Coral Gables, Florida  rises 76 feet at a 30° angle as shown in the diagram below. Find the distance d a person travels on the escalator stairs. 

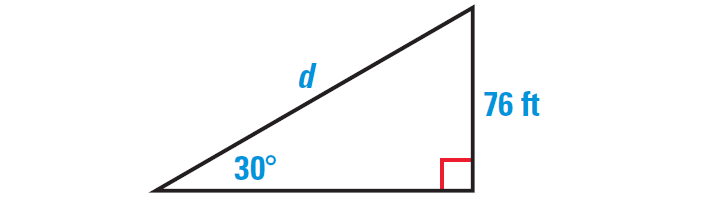
Solution :

To find the distance d a person travels on the escalator stairs, we can write a trigonometric ratio that involves the side has length d and the known length of 76 feet.

In the above right triangle, for the angle 30°, d is hypotenuse and the side has length 76 feet is opposite side. 

The trigonometric ratio that involves opposite side and hypotenuse is sin. 

Write ratio : 

sin 30°  =  opp./hyp.

Substitute. 

sin 30°  =  76/d

Multiply each side by d. 

d ⋅ sin 30°  =  76

Substitute 0.5 for sin 30°.

d ⋅ 0.5  =  76  

Divide each side by 0.5

d  =  76/0.5

d  =  152

So, the person travels 152 feet on the escalator stairs. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.