TEST FOR CONGRUENCE OF TRIANGLES

Two triangles are congruent if they are identical except for position.

Simply, If one triangle was cut with scissors and placed on the top of the other, they would match each other perfectly.

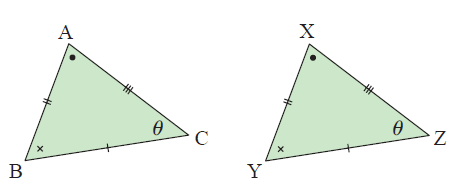
The above triangles are congruent.

We write ΔABC ≅ ΔXYZ

where ≅ reads “is congruent to”.

Test for Congruence triangles

Two triangles are congruent if one of the following is true :

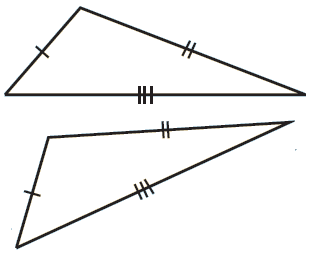
All corresponding sides are equal in length (SSS)

SSS

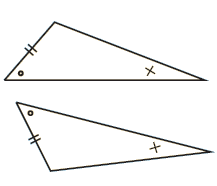
Two sides and the included angle are equal (SAS)

SAS

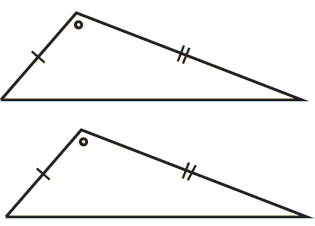Two angles and a pair of corresponding sides are equal.

AA

For right angled triangles, the hypotenuses and one pair of sides are equal (RHS)

RHS

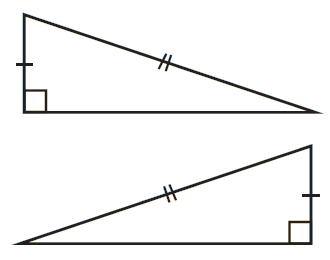Are the following pairs of triangles are congruent ? If so, state the congruence relationship and give a brief reason.

Example 1 :

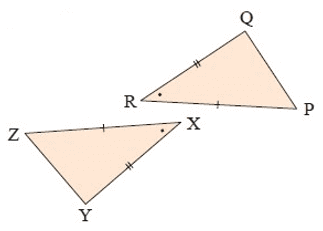
Solution :

In the given ∆PQR and ∆XYZ,

PR = ZX (Sides)

∠PRQ = ∠ZXY (Angles)

RQ = XY (Sides)

So, ∆PRQ ≅ ∆ZXY

Using SAS congruence Postulate

Example 2 :

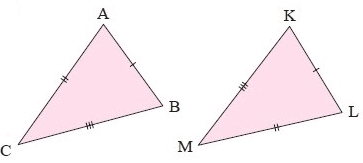
Solution :

In the given ∆ABC and ∆KLM,

AB = KL (Sides)

AC = LM (Sides)

BC = KM (Sides)

So, ∆ABC ≅ ∆KLM

Using SSS congruence Postulate

Example 3 :

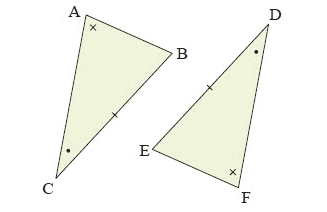
Solution :

In the given ∆ABC and ∆FED,

∠C = ∠D (Angles)

∠A = ∠F (Angles)

BC = ED (Sides)

BC and ED are corresponding sides opposite to x.

So, ∆ABC ≅ ∆FED

Using AAcorS congruence Postulate

Example 4 :

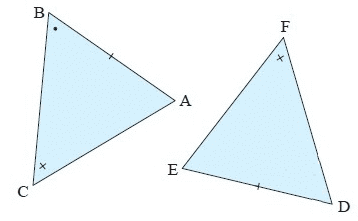
Solution :

In the given ∆ABC and ∆EDF,

∠B = ∠D (Angles)

∠C = ∠F (Angles)

AB = ED  (Sides are corresponding to the angles)

So, ∆ABC ≅ ∆EFD

Using AAcorS congruence postulate

Example 5 :

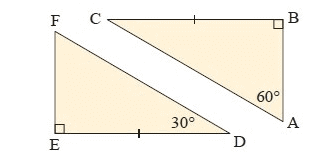
Solution :

In the given ∆ABC and ∆FED,

∠B = ∠E (Angles)

∠DEF + ∠EDF + ∠EFD = 180°

90° + 30° + ∠EFD = 180°

∠EFD = 180° - 120°

∠EFD = 60°

∠A = ∠F (Angles)

BC = ED (Sides)

which is opposite to the angles ∠A = ∠F

So, ∆ABC ≅ ∆EFD

Using AAcorS congruence Postulate

Example 6 :

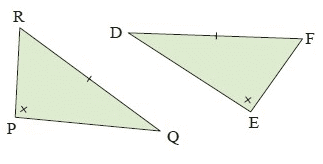
Solution :

In the given ∆PQR and ∆FED,

Here the only one pair of angles and sides are the same, so it's not congruent triangles.

So, ∆PQR ≇ ∆FED

Example 7 :

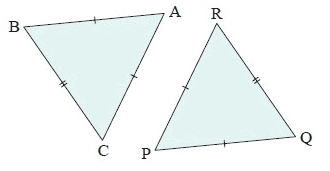
Solution :

In the given ∆ABC and ∆PQR,

AB = PR (Sides)

AC = PQ (Sides)

BC = RQ (Sides)

So, ∆ABC ≅ ∆PQR

Using SSS congruence postulate

Example 8 :

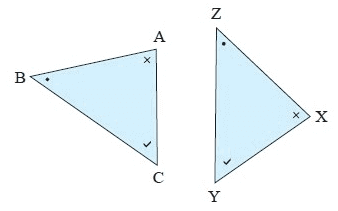
Solution :

In the given ∆ABC and ∆XYZ.

Here all the angles are equal, then triangles are also similar but not congruent triangles.

So, ∆ABC ≇ ∆XYZ

Example 9 :

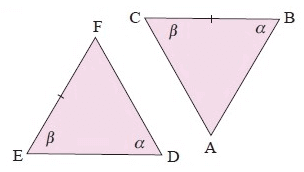
Solution  :

In the given ∆ABC and ∆EFD

∠D = ∠B = α (Angles)

∠E = ∠C = β (Angles)

But EF and BC are not equal to corresponding sides.

So, ∆ABC ≇ ∆EFD

Example 10 :

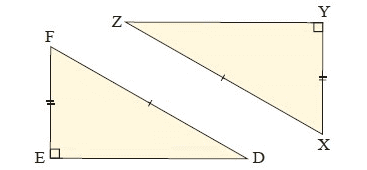
Solution :

In the given ∆DEF and ∆ZYX.

∠E = ∠Y (Right Angles)

FD = ZX (Hypotenuse sides)

EF = YX  (Sides)

So, ∆DEF ≅ ∆ZYX

Using RHS congruence postulate

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.