SYMMETRY PROPERTY OF CONGRUENCE

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

When two shapes or figures have the same shape and size, we use the term congruence and they shapes or figures are said to be congruent (≅).

In geometry, the symmetry property of congruence states that if shape 1 is congruent to shape 2, then shape 2 is also congruent to shape 2.

Similarly, if line segment AB is congruent to line segment CD, then CD is also congruent to AB.

An also, if ∠A is congruent to ∠B, then ∠B is also congruent to ∠A.

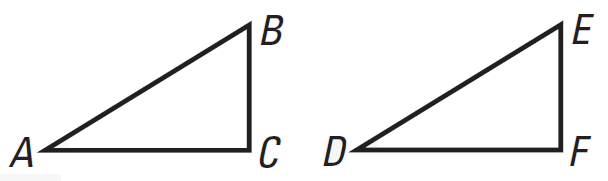
In the diagram above,

if ΔABC ≅ ΔDEF, then

ΔDEF ≅ ΔABC

Example :

In the diagram given below, triangle ABD is congruent to triangle BCD. Is triangle BCD congruent to triangle ABC ? Explain your reasoning.

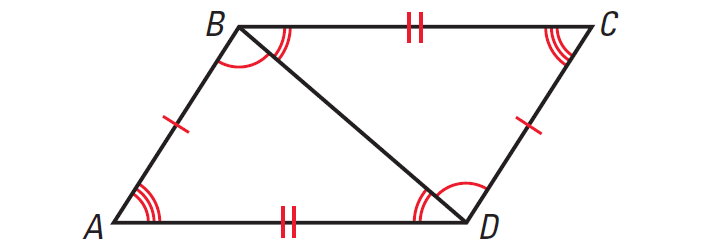
Solution :

Yes, triangle BCD is congruent to triangle ABC.

By Symmetry Property of Congruent Triangles,

if ΔABD ≅ ΔBCD, then

ΔBCD ≅ ΔABD.

Thus, triangle BCD is congruent to triangle ABC

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

Recent Articles