SURFACE AREA AND VOLUME OF COMBINED SOLIDS WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Question 1 :
A vessel is in the form of a hemispherical bowl mounted by a hollow cylinder. The diameter is 14 cm and the height of the vessel is 13 cm. Find the capacity of the vessel.
Question 2 :
Nathan, an engineering student was asked to make a model shaped like a cylinder with two cones attached at its two ends. The diameter of the model is 3 cm and its length is 12 cm. If each cone has a height of 2 cm, find the volume of the model that Nathan made.
Question 3 :
From a solid cylinder whose height is 2.4 cm and the diameter 1.4 cm, a cone of the same height and same diameter is carved out. Find the volume of the remaining solid to the nearest cm3.
Question 4 :
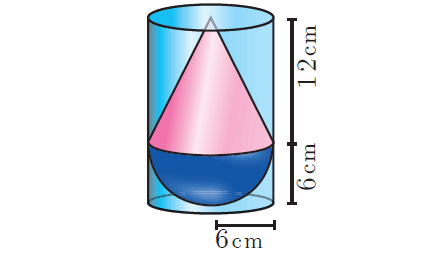
A solid consisting of a right circular cone of height 12 cm and radius 6 cm standing on a hemisphere of radius 6 cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of the water displaced out of the cylinder, if the radius of the cylinder is 6 cm and height is 18 cm.
Question 5 :
A roof is shaped like a square pyramid. One bundle of shingles covers 25 square feet. How many bundles should you buy to cover the roof ?
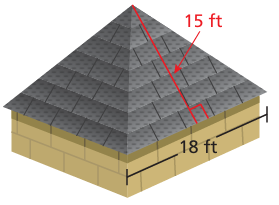
Question 6 :
You are making an umbrella that is shaped like a regular octagonal pyramid.
a. Estimate the amount of fabric that you need to make the umbrella.
b. The fabric comes in rolls that are 72 inches wide. You don’t want to cut the fabric “on the bias.” Find out what this means. Then draw a diagram of how you can cut the fabric most efficiently.
c. How much fabric is wasted?
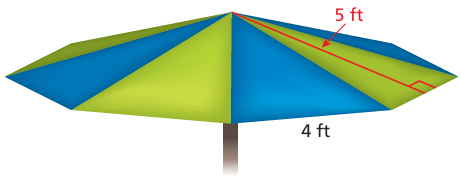
Question 7 :
Find the surface area of the cylinder. Round your answer to the nearest tenth.
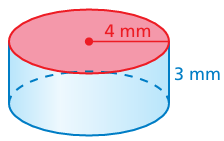
Question 8 :
Two liters of water are poured into an empty vase shaped like an octagonal prism. The base area is 100 square centimeters. What is the height of the water? (1 L = 1000 cm3)
Question 9 :
What is the approximate surface area of a cylinder with a radius of 3 inches and a height of 10 inches?
a) 30 in2 b) 87 in2 c) 217 in2 d) 245 in2
Answer Key
1) 1642.67 cm3
2) Volume of model = 66 cm3
3) 2.46 cm3
4) 1131.42 cm3
5) Approximately 22 bundles is needed.
6) a) 11520 square inches.
b) 11520
c) There is no wasted fabric in this scenario as the entire piece of fabric is used.
7) The surface area is about 175.8 square millimeters.
8) the required height is 20 cm.
9) Approximately 245 square inches. Option d is correct.
Question 1 :
A capsule is in the shape of a cylinder with two hemisphere stuck to each of its ends. If the length of the entire capsule is 12 mm and the diameter of the capsule is 3 mm, how much medicine it can hold?
Question 2 :
As shown in figure a cubical block of side 7 cm is surmounted by a hemisphere. Find the surface area of the solid.
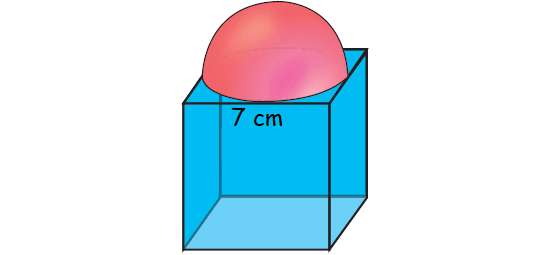
Question 3 :
A right circular cylinder just enclose a sphere of radius r units. Calculate
(i) the surface area of the sphere
(ii) the curved surface area of the cylinder
(iii) the ratio of the areas obtained in (i) and (ii)
Question 4 :
A shuttle cock used for playing badminton has the shape of a frustum of a cone is mounted on a hemisphere. The diameters of the frustum are 5 cm and 2 cm. The height of the entire shuttle cock is 7 cm. Find its external surface area.
Example 5 :
A quart of paint covers 80 square feet. How many quarts should you buy to paint the ramp with two coats? (Assume you will not paint the bottom of the ramp.)
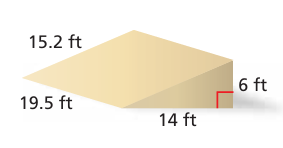
Question 6 :
A cone with radius 3 ft and height 10 ft has a volume of 30π. What is the volume of the cone formed when the following happens to the original cone?
a. The radius is doubled.
b. The height is doubled.
c. The radius and the height are both doubled.
Question 7 :
Builders use a plumb bob to find a vertical line. The plumb bob shown at the right combines a regular hexagonal prism with a pyramid. Find its volume to the nearest cubic centimeter.
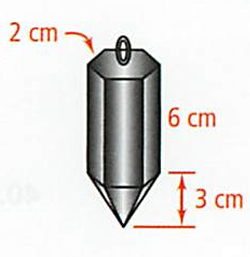
Answer Key
1) 77.78 cm3
2) 332.5 cm2
3) 1 : 1
4) 74.26 cm2
5) Approximately 6 quarts is needed.
6) a) New volume becomes 4 times of old.
b) New volume will become two times of old.
c) New volume becomes 8 times of old.
7) 54√3 cm3
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 29)
Mar 01, 26 07:26 PM
Digital SAT Math Problems and Solutions (Part - 29) -
Digital SAT Math Problems and Solutions (Part - 28)
Mar 01, 26 06:25 PM
Digital SAT Math Problems and Solutions (Part - 28) -
Digital SAT Math Problems and Solutions (Part -27)
Feb 28, 26 07:46 PM
Digital SAT Math Problems and Solutions (Part -27)