SURFACE AREA AND VOLUME OF COMBINATION OF SOLIDS QUESTIONS

Question 1 :

A capsule is in the shape of a cylinder with two hemisphere stuck to each of its ends. If the length of the entire capsule is 12 mm and the diameter of the capsule is 3 mm, how much medicine it can hold?

Solution :

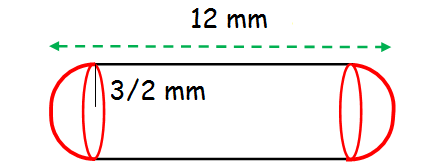
Capacity of capsule 

  =  2 Volume of hemisphere + volume of cylinder 

  =  2(2/3) πr³ + πr²h

  =  (4/3) πr³ + πr²h

Height of Capsule

  =  2 (radius of hemisphere) + height of cylinder

2(3/2) + h  =  12

3 + h =  12

h  =  12 - 3  =  9

=  πr² [(4/3) r + h]

=  (22/7) (3/2)²[(4/3)(3/2) + 9]

 =  (22/7) (9/4)[2 + 9]

 =  (11/7) (9/2)(11)

=  77.78 cm³

Question 2 :

As shown in figure a cubical block of side 7 cm is surmounted by a hemisphere. Find the surface area of the solid.

Solution :

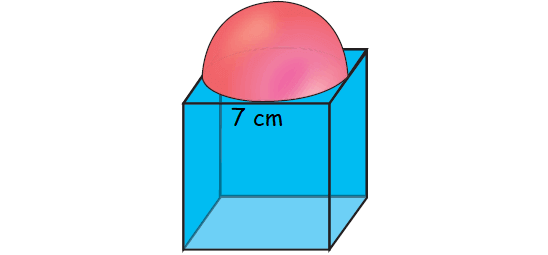
Surface area of solid 

  =  surface area of cube + curved surface area of hemisphere - area of base  of hemisphere 

  = 6a² + 2πr²  - πr² 

  = 6a² + πr²

  =  6(7)² + (22/7) (7/2)² 

  =  294 + 38.5

  =  332.5 cm²

Question 3 :

A right circular cylinder just enclose a sphere of radius r units. Calculate (i) the surface area of the sphere (ii) the curved surface area of the cylinder (iii) the ratio of the areas obtained in (i) and (ii).

Solution :

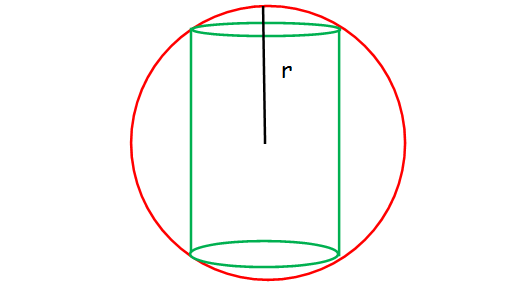
radius of sphere  =  height of cylinder/2

(i) the surface area of the sphere  =  4πr²

(ii) the curved surface area of the cylinder

  =  2π r h

  =  2π r(2r)

  =  4πr²

(iii) the ratio of the areas obtained in (i) and (ii).

  =  4πr²  : 4πr²

  =  1 : 1

Question 4 :

A shuttle cock used for playing badminton has the shape of a frustum of a cone is mounted on a hemisphere. The diameters of the frustum are 5 cm and 2 cm. The height of the entire shuttle cock is 7 cm. Find its external surface area.

Solution :

Surface area of shuttle cock  =  curved surface area of frustum cone + curved surface area of hemisphere

  =  π (R + r) l + 2πr²  ----(1) 

Height of shuttle cock  =  7

radius of hemisphere + height of frustum cone  =  7

1 + h  =  7

h  =  6

l = √(h² + (R - r)²)

l = √(6² + ((5/2) - 1)²)

l = √(36 + (9/4)

l = √153/2

l = 12.36/2

l = 6.18

By applying the value of l in (1), we get 

  =  π ((5/2) + 1) l + 2πr²

  =  π[(7/2)(6.18) + 2 (1)²]

  =  (22/7)[(21.63 + 2]

  =  74.26 cm²

Example 6 :

A quart of paint covers 80 square feet. How many quarts should you buy to paint the ramp with two coats? (Assume you will not paint the bottom of the ramp.)

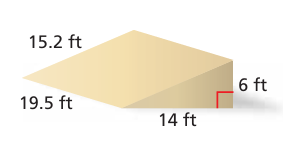
Solution :

1 quart = 80 square feet

In triangular base,

base = 6 ft, height = 14 ft and height of prism = 19.5 ft

Surface area of prism = 2 area of rectangle + area of base rectangle + 2 x area of triangle

Area of rectangle left and right = 19.5 x 15.2

= 296.4 square ft

Area of rectangle at bottom = 15.2 x 6

= 91.2 square ft

Area of triangular faces = 2 x (1/2) x 14 x 6

= 84 square ft

Required area = 296.4 + 91.2 + 84

= 471.6 square feet

Number of quarts required = 471.6/80

= 5.895

Approximately 6 quarts is needed.

Example 7 :

A cone with radius 3 ft and height 10 ft has a volume of 30π. What is the volume of the cone formed when the following happens to the original cone?

a. The radius is doubled.

b. The height is doubled.

c. The radius and the height are both doubled.

Solution :

Volume of given cone = 30π

a) Given radius = 3 ft, when it is doubled then the new radius = 6 ft

Volume of new cone = (1/3) πr² h

= (1/3) x π x 6² x 10

= 120π cubic ft

New volume becomes 4 times of old.

b) Given height = 10 ft, when it is doubled, then the new height = 20 ft

Volume of new cone = (1/3) πr² h

= (1/3) x π x 3² x 20

= 60π cubic ft

New volume will become two times of old.

c) New radius = 6 ft, new height = 20 ft

Volume of new cone = (1/3) πr² h

= (1/3) x π x 6² x 20

= 240π cubic ft

New volume becomes 8 times of old.

Example 8 :

Builders use a plumb bob to find a vertical line. The plumb bob shown at the right combines a regular hexagonal prism with a pyramid. Find its volume to the nearest cubic centimeter.

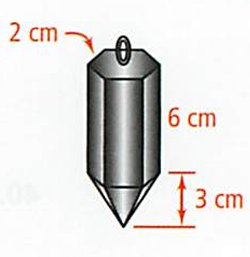
Solution :

In a hexagon, we can create 6 equilateral triangles.

Area of equilateral triangle = (√3/4) a²

Here a = 2 cm

Area of hexagon = 6 (√3/4) ⋅ 2²

base area = 6√3 square cm

Volume of hexagonal prism = base area x height

= 6√3 ⋅ 6

= 36√3 cm³

Volume of bottom hexagonal base prism = 6√3  ⋅ 3

= 18√3 cm³

Total volume = (36√3 + 18√3) cm³

= 54√3 cm³

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.