SPHERE

Definition of Sphere :

This is a solid generated when a semicircle is being rotated about its diameter. In three dimensional space, this is also known as perfect round geometrical object.

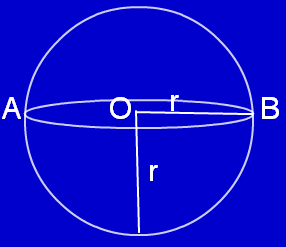
A plane is at the center of the spherical solid divides the solid in to two equal parts. Each shape is called hemisphere.

Example :

A very good example we can say for spherical shaped solid is globe. Ball is another good example for spherical shaped solid.

Curved surface area A  =  4πr²

Volume of sphere  =  (4/3)πr³

Example 1 :

The formula for calculating the total surface area A of a sphere of radius r is A  =  4πr². 

Find:

a) the total surface area of a sphere of radius 7.5 cm

b) the radius, in cm, of a spherical balloon which has a surface area of 2 m².

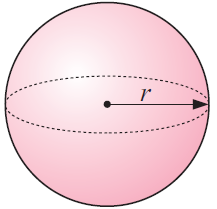
Solution :

Radius  =  7.5 cm

Total surface area of the sphere  A  =  4πr²

=  4π(7.5)²

=  225π cm²

So, the total surface area of the sphere is 225π cm².

Example 2 :

A sphere of radius r has volume given by 

V  =  (4/3)πr³

Find :

a) the volume of a sphere of radius 2.37 m

b) the radius of a sphere that has volume 2500 cm³.

Solution : 

(a)  Volume of sphere (V ) =  (4/3)πr³

Radius (r)  =  2.37 m

=  (4/3)π(2.37)³

=  (4/3)π(133.12)

=  177.49 π cm³

(b)  Volume of sphere  =  2500 cm³

(4/3)πr³  =  2500

r³  =  2500/4.18

r  =  8.42 

Example 3 :

A spherical art piece has diameter 2 meters. Find 

(a)  The surface area of the sphere 

(b)  The cost of painting the sphere (with 3 coats) given each square meter will cost $13.50 for paint and labour.

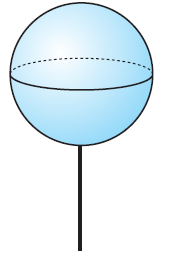
Solution :

Diameter (a)  =  2 m and radius  =  1 m

(a)  Surface area of sphere  =  4πr²

=  4π(1)²

=  4π cm²

(b)  Cost of painting  =  $13.50

Cost for 1 coat  =  4π (13.50)

=  54π

=  54 x 3.14

=  169.56

Cost for 3 coats  =  3(169.56)

=  $508.68

So, the required cost is $508.68.

Example 4 :

Find the size of the radius in each of the spheres below. Give your answers to one decimal place

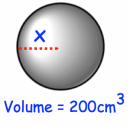
Solution :

Volume of sphere = (4/3)πr³

Here r = x cm

200 = (4/3)πx³

200 x (3/4) x 1/3.14 = x³

x³ = 47.7

x = 3.6 cm

Example 5 :

A metal cuboid measuring 4cm by 5cm by 12cm is melted down and a sphere is made. Calculate the radius of the sphere.

Solution :

Since the cuboid is melted and made a sphere, the volume of cuboid and sphere both will be equal.

Volume of cuboid = volume of sphere

l x b x h = (4/3)πr³

4 x 5 x 12 = (4/3)πr³

r³ = 4 x 5 x 12 x (3/4) x 1/3.14

r³ = 57.32

r = 3.85 cm

So, the radius of the sphere is 3.85 cm.

Example 6 :

Julie thinks that if you double the radius of the sphere shown at the right, the surface area will double. Is she right? Explain your reasoning

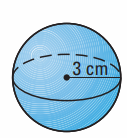
Solution :

From the given figure, the radius of the sphere = 3 cm

When we double the radius, the new radius will be 6 cm.

Surface area of having the radius of 3 cm.

= 4πr²

= 4π(3)²

= 36 π cm²

Surface area of having the radius of 6 cm.

= 4π (6)²

= 144 π cm²

When we double the radius the surface area will not become twice. So, her argument is not correct.

Example 7 :

Estimate the volume of air in a beach ball that has a 12 inch diameter. Round your answer to the nearest whole number.

Solution :

Diameter = 12 inch

Radius of sphere = 6 inches

Volume of hemisphere = (2/3)πr³

= (2/3)π(6)³

= 2/3 x 3.14 x 216

= 452.16 cubic inches.

Example 8 :

Find the volume of a sphere whose surface area is 154 cm² .

Solution :

Surface area of sphere = 154 cm²

2πr² = 154

2 x 22/7 x r² = 154

r² = 154 x (7/22) x (1/2)

r² = 24.5

r = 4.94 cm

r = 5 cm approximately

Example 9 :

A capsule of medicine is in the shape of a sphere of diameter 3.5 mm. How much medicine (in mm³ ) is needed to fill this capsule?

Solution :

Diameter of the sphere = 3.5 mm

Radius of the sphere = 1.75 mm

Volume of sphere = (4/3)πr³

= (2/3)π(1.75)³

= 3.57 π mm³

Example 10 :

The diameter of a sphere is decreased by 25%. By what % does its volume decreased.

Solution :

Diameter of the sphere = D

radius of the sphere = D/2

Volume of sphere = (4/3)π(D/2)³

= (4/3)π(D³/8)

= πD³/6

New radius of the sphere = 75% of (D/2)

= 0.75D/2

= 0.375 D

Volume of the sphere = (4/3)πr³

= (4/3)π(0.375D)³

= 0.05(4/3)πD³

= (5/100)(4/3)πD³

= 0.05(4) (πD³/3)

= 0.05(4) (2/2) (πD³/3)

= 0.4 (1/2) (πD³/3)

= 40% of (πD³/6)

So, 60% is reduced.

Example 11 :

The volumes of two hemispheres are in the ratio 27:125. Find the ratio of the radii.

Solution :

Let r1 and r2 be radii of two hemispheres.

(2/3)πr₁³ : (2/3)πr₂³ = 27 : 125

r₁³ : r₂³ = 27 : 125

r₁³ : r₂³ = 3³ : 5³

So, the ratio between their radii is 3 : 5.

Related Pages

• How to find volume of sphere
• Volume of sphere practice problems 
• Surface area and volume of spheres
• Curved surface area and total surface area of sphere and hemisphere
• Examples on volume of sphere and hemisphere
• Volume of sphere and hemisphere worksheet

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.