SOLVING PROBLEMS USING ROLLES THEOREM

Let f (x) be continuous on a closed interval [a, b] and differentiable on the open interval (a, b)

If f(a)  =  f(b)

then there is at least one point c ∈ (a,b) where f '(c) = 0.

Geometrically this means that if the tangent is moving along the curve starting at x = a towards x = b then there exists a c ∈ (a, b) at which the tangent is parallel to the x -axis.

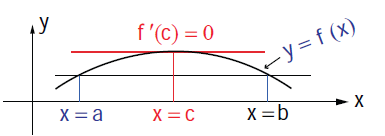
Using the Rolle’s theorem, determine the values of x at which the tangent is parallel to the x -axis for the following functions :

Problem 1 :

f(x)  =  x² − x, x ∈ [0, 1]

Solution :

f(x) is defined and continuous on the closed interval [0, 1] and it is differentiable on (0, 1).

(1)  =  (2)

So, there is at least one point c ∈ [0, 1]

f'(c) =  2x-1

2c-1  =  0

2c  =  1

c  =  1/2

Problem 2 :

f(x)  =  (x² - 2x)/(x + 2), x ∈ [-1, 6]

Solution :

f(x) is defined and continuous on the closed interval [-1, 6] and it is differentiable on (-1, 6).

(1)  =  (2)

So, there is at least one point c ∈ [-1, 6]

f'(x)  =  [(x+2) (2x-2) - (x²-2x) (1)] / (x+2)²

f'(x)  =  (2x²+2x-4 - x²+2x) / (x+2)²

f'(x)  =  (x²+4x-4) / (x+2)²

f'(x)  =  0

x² + 4x - 4  =  0

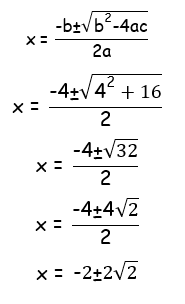
So, the solutions are -2±2√2.

Problem 3 :

f(x)  =   √x - (x/3), x∈ [0, 9]

Solution :

f(x) is defined and continuous on the closed interval [0, 9] and it is differentiable on (0, 9).

(1)  =  (2)

So, there is at least one point c ∈ [-1, 6]

f(x)  =   √x - (x/3)

f'(x)  =   1/2√x - (1/3)

1/2√x - (1/3)  =  0

1/2√x  =  1/3

3  =  2√x

√x  =  3/2

x  =  9/4 ∈ [-1, 6]

For each problem, find the values of c that satisfy Rolle's Theorem.

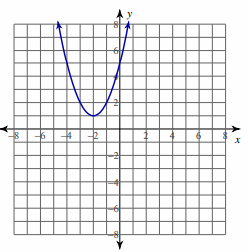
Problem 4 :

y = x² + 4x + 5; [−3, −1]

Solution :

i)  The given function y is defined and continuous on the closed interval [-3, -1].

ii) Let f(x) = y = x² + 4x + 5

f'(x) = 2x + 4(1) + 0

f'(x) = 2x + 4

It is differentiable in the open interval (-3, -1).

iii) 

f(-1) = f(-3)

So, there must be c in the interval [-3, -1].

f'(c) = 0

2c + 4 = 0

2c = -4

c = -4/2

c = -2

So, the value of c is -2.

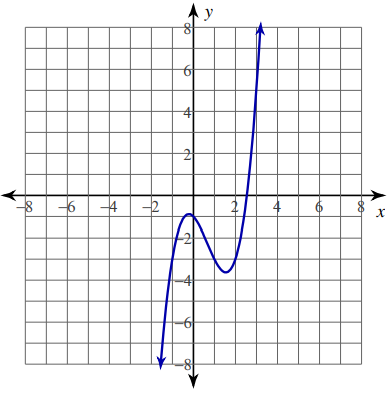
Problem 5 :

y = x³ - 2 x² - x - 1; [−1, 2]

Solution :

i)  The given function y is defined and continuous on the closed interval [-1, 2].

ii) Let f(x) = y = x³ - 2 x² - x - 1

f'(x) = 3x² - 2(2x) - 1 - 0

f'(x) = 3x² - 4x - 1

It is differentiable in the open interval (-1, 2).

iii) f(x) = x³ - 2 x² - x - 1

f(-1) = (-1)³ - 2 (-1)² - (-1) - 1

= -1 - 2 + 1 - 1

= -3 ----(1)

f(2) = 2³ - 2 (2)² - 2 - 1

= 8 - 2(4) - 2 - 1

= 8 - 8 - 3

= -3 -----(2)

It satisfies all the condition, so there must be c in the interval [-1, 2].

3x² - 4x - 1 = 0

Solving this quadratic equation using formula, 

a = 3, b = -4 and c = -1

= (-b ± √b² - 4ac)/2a

= 4 ± [√(-4)² - 4(3)(-1)]/2(3)

= 4 ± [√(16 + 12)]/6

= 4 ± √28/6

= (4 ± 2√7)/6

= (2 ± √7)/3

So, the required values of c are (2 + √7)/3 and (2 - √7)/3.

Problem 6 :

y = -2 sin (2x) [−π, π]

Solution :

i)  The given function y is defined and continuous on the closed interval [−π, π]

ii) Let f(x) = y = -2 sin (2x)

f'(x) = -2 cos (2x)(2)

f'(x) = -4 cos 2x

It is differentiable in the open interval (−π, π).

iii) f(x) = -2 sin (2x)

f(−π) = -2 sin (-2π)

= 2 sin (2π)

= 2(0)

= 0 -----(1)

f(π) = -2 sin (2π)

= -2 sin (2π)

= -2(0)

= 0 -----(2)

(1) = (2)

It satisfies all the condition, so there must be c in the interval [-π, π].

-4 cos 2x = 0

cos (2x) = 0

2x = cos^-1(0)

2x = -π/2,  -3π/2, π/2, 3π/2

x = -π/4,  -3π/4, π/4, 3π/4

Problem 7 :

y = cos (2x) [π/3, 2π/3]

Solution :

i)  The given function y is defined and continuous on the closed interval [π/3, 2π/3]

ii) Let f(x) = y = cos (2x)

f'(x) = -sin (2x)(2)

f'(x) = -2 sin 2x

It is differentiable in the open interval [π/3, 2π/3]

iii) f(x) = cos (2x)

f(π/3) = cos (2π/3)

= -1/2 -----(1)

f(2π/3) = cos (4π/3)

= cos (π + π/3)

= cos π/3

= -1/2 -----(2)

It satisfies all the condition, so there must be c in the interval [π/3, 2π/3].

-2 sin 2x = 0

sin (2x) = 0

2x = sin^-1(0)

2x = π, 2π

x = π/2, 2π/2

x = π/2, π

So, the value of c is π/2.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.