SOLVING INEQUALITIES BY MULTIPLYING OR DIVIDING
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Remember, solving inequalities is similar to solving equations. To solve an inequality that contains multiplication or division, undo the operation by dividing or multiplying both sides of the inequality by the same number.
The rules below show the properties of inequality for multiplying or dividing by a positive number.
Multiplication by Positive Numbers
Words :
Both sides of an inequality can be multiplied by the same positive number, and the statement will still be true.
Numbers :
5 < 8
5(3) < 8(3)
15 < 24
Algebra :
If x < y and z > 0, then,
xz < yz
Division by Positive Numbers
Words :
Both sides of an inequality can be multiplied by the same positive number, and the statement will still be true.
Numbers :
20 < 45
20/5 < 45/5
4 < 9
Algebra :
If x < y and z > 0, then,
x/z < y/z
Note :
The above explained properties are also true for inequalities that use the symbols >, ≥, and ≤.
Multiplying or Dividing by a Positive Number
Example 1 :
Solve the following inequality and graph the solution.
3x < 18
Solution :
3x < 18
Because x is multiplied by 3, divide each side by 3 to undo the multiplication.
3x/3 < 18/3
x < 6

Example 2 :
Solve the following inequality and graph the solution.
y/2 > -1.5
Solution :
y/2 > -1.5
Because y is divided by 2, multiply each side by 2 to undo division.
2(y/2) > 2(-1.5)
y > -3

What happens when you multiply or divide each side of an inequality by a negative number?
Look at the number line below.
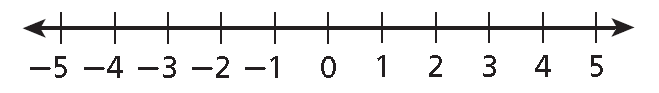
|
2 < 5 Multiply each side by -1. -2 ? -5 Use the number line to determine the direction of the inequality. -2 > -5 |
5 > -2 Multiply each side by -1. -5 ? 2 Use the number line to determine the direction of the inequality. -5 < 2 |
Notice that when you multiply (or divide) both sides of an inequality by a negative number, you must reverse the inequality symbol. This means there is another set of properties of inequality for multiplying or dividing by a negative number.
Multiplication by Negative Numbers
Words :
If each side of an inequality is multiplied by the same negative number, you have to reverse the inequality symbol for the statement to still be true.
Numbers :
8 > 5
8(-3) < 5(-3)
-24 < -15
Algebra :
If x > y and z < 0, then,
xz < yz
Division by Negative Numbers
Words :
If each side of an inequality is divided by the same negative number, you have to reverse the inequality symbol for the statement to still be true.
Numbers :
45 > 20
45/(-5) < 20/(-5)
-9 < -4
Algebra :
If x > y and z < 0, then,
x/z < y/z
Note :
The above explained properties are also true for inequalities that use the symbols >, ≥, and ≤.
Multiplying or Dividing by a Negative Number
Example 3 :
Solve the following inequality and graph the solution.
-10a > 15
Solution :
-10a > 15
Because a is multiplied by -10, divide each side by -10 and change > to <.
-10a/(-10) < 15/(-10)
a < -1.5

Example 4 :
Solve the following inequality and graph the solution.
-b/10 ≥ -0.11
Solution :
-b/10 ≥ -0.11
Because -b is divided by 10, multiply each side by -10 and change ≥ to ≤.
(-b/10)(-10) ≤ -0.11(-10)
10b/10 ≤ 1.1
b ≤ 1.1

Consumer Application
Example 5 :
James has a $16 gift card for a health store where a smoothie costs $2.50 with tax. What are the possible numbers of smoothies that James can buy?
Solution :
Let y represent the number of smoothies James can buy.
$2.50
times
number of smoothies
is at most
$16
2.50
⋅
y
≤
16
2.50y ≤ 16
Because y is multiplied by 2.50, divide each side by 2.50. The symbol does not change.
y ≤ 6.4
James can buy only a whole number of smoothies.
So, he can buy 0, 1, 2, 3, 4, 5 or 6 smoothies.
Example 5 :
Solve the inequality and graph the solution
24 + 6k < -6(-4 - k)
Solution :
24 + 6k < -6(-4 - k)
Distributing -6, we get
24 + 6k < 24 + 6k
Subtracting 24 and subtracting 6k, we get
24 - 24 < 6k - 6k
0 < 0
So, there is no solution.
Example 6 :
Solve the inequality and graph the solution
-4(4 + 7x) + x ≥ -6x + 5
Solution :
-4(4 + 7x) + x ≥ -6x + 5
Distributing -4, we get
-16 - 28x + x ≥ -6x + 5
-16 - 27x ≥ -6x + 5
Adding 6x on both sides
-27x + 6x - 16 ≥ 5
Adding 16 on both sides
-21x ≥ 5 + 16
-21x ≥ 21
When we divide by negative sign on both sides of the inequality, we get
x ≤ -1
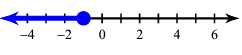
Example 7 :
Tom is deciding whether or not he should become a member gym to use their basketball courts. The membership cost is $135. Members pay $2 to rent out the basketball courts. Non-members can rent the court also, but they have to pay $11 each time. how many times would Tom need to rent the court in order for it be cheaper to be a member than a non member?
Solution :
Membership cost = $135
Rent per hour for members = $2
Rent for non members = $11
Let x be the number of hours renting.
Rent paid by members for renting x hours = 135 + 2x
Rent paid by non members for renting x hours = 11x
135 + 2x < 11x
To solve for x, we have to subtract 2x on both sides.
135 < 11x - 2x
135 < 9x
Dividing by 9 on both sides
135/9 < x
15 < x
At least 15 times.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 38)
Dec 29, 25 04:21 AM
10 Hard SAT Math Questions (Part - 38) -
10 Hard SAT Math Questions (Part - 39)
Dec 28, 25 11:20 PM
10 Hard SAT Math Questions (Part - 39) -
10 Hard SAT Math Questions (Part - 41)
Dec 28, 25 06:05 PM
10 Hard SAT Math Questions (Part - 41)

