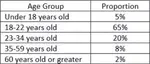
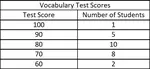
SOLVING ALGEBRAIC WORD PROBLEMS WITH EQUATIONS

Problem 1 :

At t minutes past 2 pm, the time needed to 3 pm is 3 minutes less than t²/4. Find t.

Solution :

Given time needed by the minutes hand show (t²/4) – 3

Hence the quadratic equation becomes, (t²/4) – 3 = 60 – t

(t² – 12)/4 = 60 – t

(t² – 12) = 240 – 4 t

t² – 12 – 240 + 4 t = 0

t² + 4t – 252 = 0

t² + 18t – 14t – 252 = 0

t(t + 18) – 14(t + 18) = 0

(t + 18)(t – 14) = 0

(t + 18) = 0 or (t – 14) = 0

t = - 18 or t = 14

Since "t" cannot be negative, t = 14 

Problem 2 :

The number of seats in a row is equal to the total number of rows in a hall. The total number of seats in the hall will increase by 375 if the number of rows is doubled and the number of seats in each row is reduced by 5. Find the number of rows in the hall at the beginning

Solution :

Let the numbers of rows be x

So the number of seat in each row will also be x

So the total number of seats in the auditorium  =  x²

When the number of rows is doubled and the number of seats in each rows is decreased by 5

so now the total number of seat in the auditorium will be

   =  2x(x-5)

  =  2x²-10x

given

2x²- 10x - x² = 375

x²- 10x - 375 = 0

(x - 25) (x + 15)  =  0

x  =  25 and x  =  -15

The number of seats will not be negative. Hence the number of rows was initially is 25.

Problem 3 :

If a and b are the roots of the polynomial f(x) = x² −2x + 3, find the polynomial whose roots are

(i) α + 2, β + 2

(ii)  (α - 1)/(α + 1), (β - 1)/(β + 1)

Solution :

f(x) = x² − 2x + 3

f(x)  =  (x - 1) (x - 2)

x - 1 = 0 and x - 2  =  0

x  =  1 and x = 2

α = 1, β = 2

α + 2  =  1 + 2  =  3

β + 2  =  2 + 2  =  4

Now, we have to find the quadratic equation whose roots are 3 and 4.

x² - (α + β) x + αβ  =  0

x² - (3 + 4) x + 3(4)  =  0

x² - 7x + 12  =  0

(ii)  (α - 1)/(α + 1), (β - 1)/(β + 1)

(α - 1)/(α + 1)  =  (3 - 1)/(3 + 1)  =  2/4  =  1/2

(β - 1)/(β + 1)  =  (2 - 1)/(2 + 1)  =  1/3

Now, we have to find the quadratic equation whose roots are (α - 1)/(α + 1), (β - 1)/(β + 1)

x² - ((1/2) + (1/3)) x + (1/2)(1/3)  =  0

x² - (5x/6) + (1/6) =  0

6x² - 5x + 1  =  0

If –4 is a root of the equation x² + px −4 = 0 and if the equation x² + px +q = 0 has equal roots, find the values of p and q.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.