SOLVED PROBLEMS ON DETERMINANTS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
Without expanding the determinant, prove that
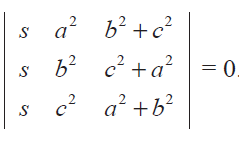
Problem 2 :
Show that
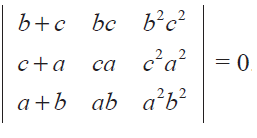
Problem 3 :
Prove that
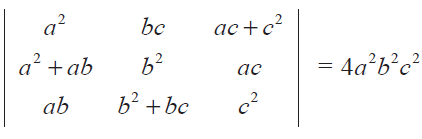
Problem 4 :
Prove that
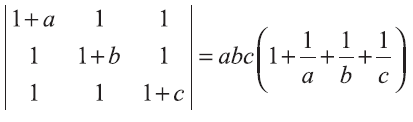
Problem 5 :
Prove that
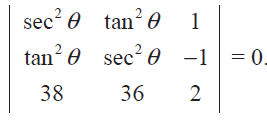
Problem 6 :
Show that
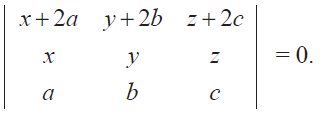
Problem 7 :
Write the general form of a 3 × 3 skew-symmetric matrix and prove that its determinant is 0. Solution
Problem 8 :
If
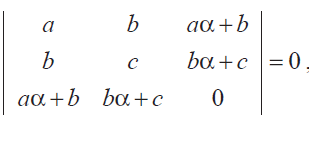
prove that a, b, c are in G.P. or a is a root of ax2 + 2bx + c = 0. Solution
Problem 9 :
prove that
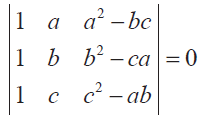
Problem 10 :
If a, b, c are pth, qth and rth terms of an A.P, find the value of
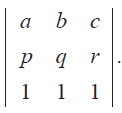
Problem 11:
Prove that
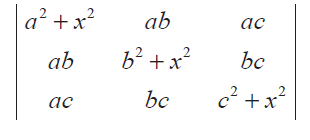
Problem 12 :
If a, b, c are all positive, and are pth, qth and rth terms of a G.P., show that
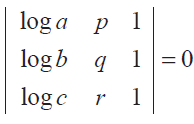
Problem 13 :
Find the value of
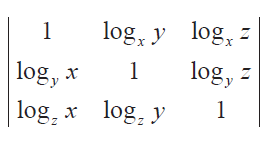
if x, y and z ≠ 1 Solution
Problem 14 :
If A =
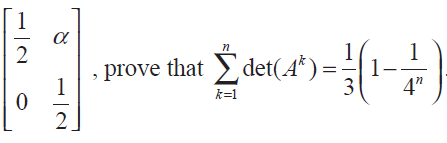
Problem 15 :
Without expanding, evaluate the following determinants
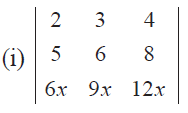
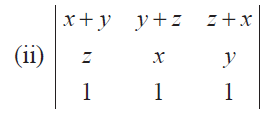
Problem 16 :
If A is a square matrix and | A | = 2, find the value of |AAT| . Solution
Problem 17 :
If A and B are square matrices of order 3 such that | A | = -1 and |B| = 3, find the value of |3AB|. Solution
Problem 18 :
If λ = - 2, determine the value of
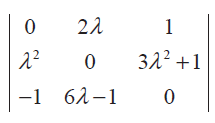
Problem 19 :
Determine the roots of the equation
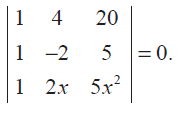
Problem 20 :
Verify that det(AB) = (det A) (det B) for
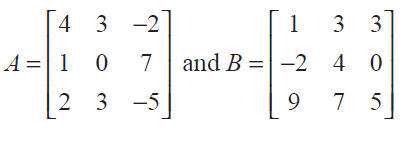
Problem 21 :
Using cofactors of elements of second row, evaluate | A |, where
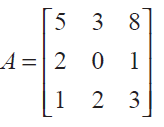
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4)
