MATRIX AND DETERMINANTS EXAMPLE PROBLEMS

About "Matrix Determinant Example Problems"

Matrix Determinant Example Problems :

Here we are going to see some example problems to understand solving determinants using properties.

To know properties of determinants, please visit the page "Properties of determinants".

Matrix Determinant Example Problems - Questions

Question 1 :

Prove that

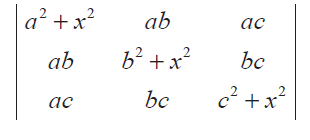
Solution :

First let us factor "a" from the 1^st row, "b" from the 2^nd row and c from the 3^rd row.

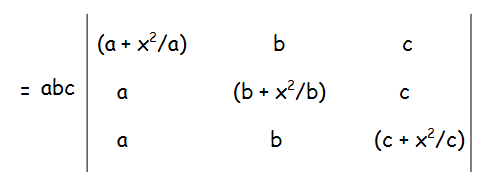
Now we have to multiply column 1, 2 and  by a, b and c respectively.

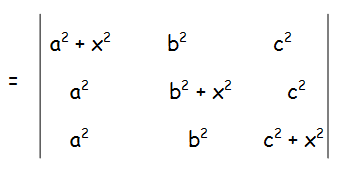
Let us subtract 2^nd row from 1^st row and subtract 3^rd row from the 2^nd row.

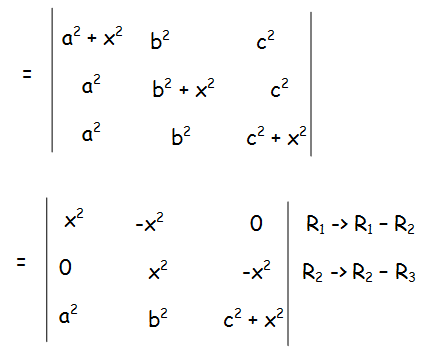
  =  x²(c²x² + x⁴ + b²x²) + x²(0 + a² x²) 

  =  x²(c²x² + x⁴ + b²x²) + x²(0 + a² x²) 

  =  x⁴ c² + x⁶ + b²x⁴ + a²x⁴

  =  x⁴(c² + x² + b²+ a²)

Hence it is divisible by x⁴.

Question 2 :

If a, b, c are all positive, and are p^th, q^th and r^th terms of a G.P., show that

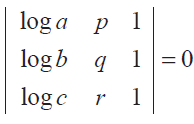
Solution :

n^th term of G.P

a_n  =  ar^n-1

a = p^th term of G.P  =  ar^p-1   --(1)

b = q^th term of G.P  =  ar^q-1   --(2)

c = r^th term of G.P  =  ar^r-1   --(3)

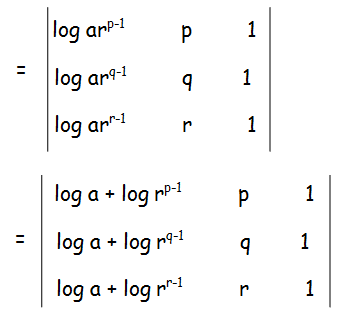
By using properties of determinants, let us write them as sum of two determinants.

In the second determinant, let us add 1^st and 3^rd column.

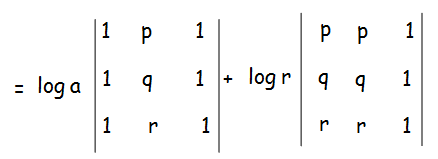
In the first determinant column 1 and  are identical. In the second determinant column 1 and 2 are identical.

  =   log a (0) + log r (0)

  =  0

Hence it is proved.

Question 3 :

Find the value of 

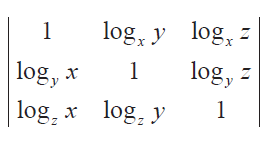
if x, y and z ≠ 1

Solution :

By expanding the above determinant, we get

  =  1[1 - log_zy log_yz] - log_xy[log_yx - log_zx log_yz] + log_xz[log_yxlog_zy - log_zx]

By using the properties of logarithms

  =  [1 - log_yy] - log_xylog_yx + log_xylog_zx log_yz + log_xzlog_yxlog_zy - log_xzlog_zx

  =  [1 - log_yy] - log_yy + log_zylog_yz + log_yzlog_zy - log_zz

  =  [1 - 1] - 1 + log_yy + log_zz - 1

  =  - 1 + 1 + 1 - 1

  =  0

Hence the answer is 0.

Question 4 :

If A =

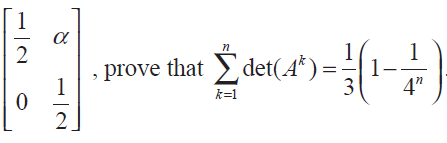
Solution :

|A|  =  1/4

det (A^k)  =  (1/4)^k

By finding the sum, we get

  =  (1/4) + (1/4)² + (1/4)³ + ..................n terms

Sum of geometric series

S_n  =   a(rⁿ - 1) / (r - 1)

a  =  1/4,  r  =  1/4

S_n  =   (1/4)((1/4)ⁿ - 1) / ((1/4) - 1)

  =   (1/4)((1/4)ⁿ - 1) / (-3/4)

  =  (-1/3) ((1/4)ⁿ - 1)

  =  (1/3)(1 - (1/4)ⁿ)

Hence it is proved.

After having gone through the stuff given above, we hope that the students would have understood, "Matrix Determinant Example Problems". 

Apart from the stuff given in "Matrix Determinant Example Problems",  if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.