SOLVING DETERMINANTS USING PROPERTIES

About "Solving Determinants Using Properties"

Solving Determinants Using Properties :

Here we are going to see some example problems to understand solving determinants using properties.

To know properties of determinants, please visit the page "Properties of determinants".

Solving Determinants Using Properties - Questions

Question 1 :

Without expanding the determinant, prove that

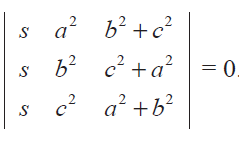
Solution :

To prove  the given determinant as zero, we may try to show any two rows or columns as identical.

For that we use elementary operations.

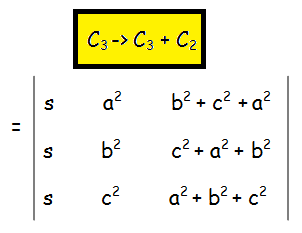
Now we may factor out "s" and  "(a² + b² + c²)" from the 1^st and and 3^rd column respectively.

So, we get

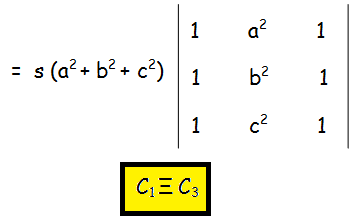
If any two columns are identical, then the value of determinant will become zero.

  =  s(a² + b² + c²) (0)

  =  0

Hence proved.

Question 2 :

Show that 

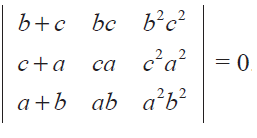
Solution :

In order to show any two rows or columns are same, let us multiply "a", "b" and "c" by the 1^st, 2^nd and 3^rd row respectively.

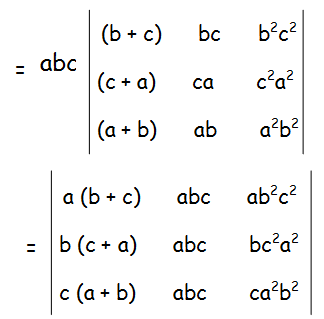
Now we may factor abc from 2^nd and 3^rd column respectively.

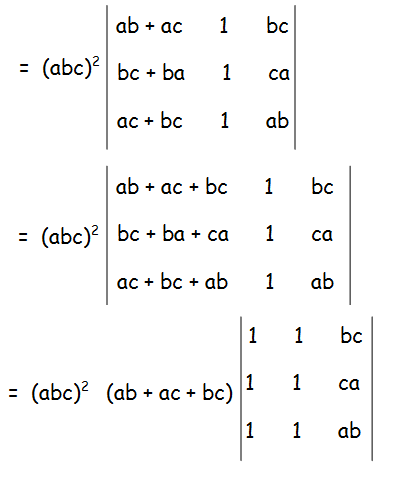
Since column 1 and 2 are identical, the value of determinant will become 0.

So, we get (abc)² (ab + bc + ca) (0).

Hence the answer is 0.

Question 3 :

Prove that

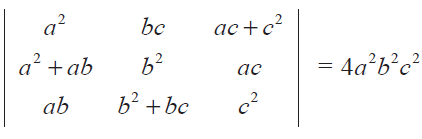
Solution :

First let us factor out a from a² + ab, b from b² + bc and c from c² + ac respectively.

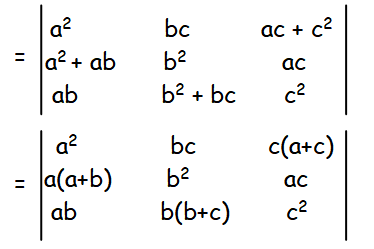
Factor out a, b and c from column 1, 2 and 3 respectively.

So, we get

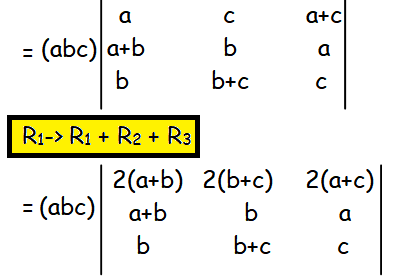
Now we may factor out 2 from the first row.So, we get

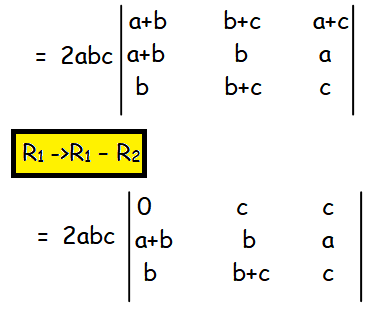
Now let us subtract column 3 from column 2. So we get

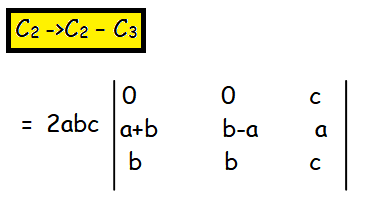
  =  2abc [ c(ab + b² - b(b - a)) ]

  =  2abc [ c(ab + b² - b² + ab) ]

  =  2abc [ 2abc ]

  =  4a²b²c²

Hence proved.

Question 4 :

Prove that

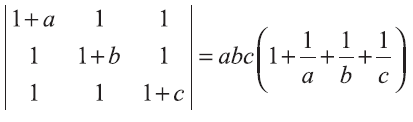
Solution :

First let us subtract second row from 1^st row.

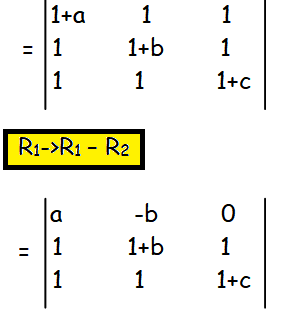
Since we cannot simplify this hereafter, let us find the expansion.

  =  a [(1+b)(1+c) - 1] + b[(1+c) - 1]

  =  a [(1 + c + b + bc) - 1] + b[1+c-1]

  =  a [c + b + bc] + b[c]

  =  ac + ab + abc + bc

  =  abc +ab + bc + ca

  =  abc (1 + 1/a  + 1/b  +  1/c)

Hence proved.

After having gone through the stuff given above, we hope that the students would have understood, "Solving Determinants Using Properties". 

Apart from the stuff given in this section,  if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.