SOLVE LINEAR INEQUALITIES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
A statement involving variable or variables and the sign of inequality like <, >, ≤ or ≥ is called an inequality.
Here we are going to see how to solve linear inequalities.
- Solving linear inequalities in one variable
- Solving linear inequalities in two variables
Linear Inequalities in One Variable
Let a be a non zero real numbers and x be a variable.
Then, the inequality of the form
ax + b < 0
ax + b ≤ 0
ax + b > 0
ax + b ≥ 0
are known as linear inequalities in one variable.
Solving Linear Inequalities in One Variable
Rule 1 :
Same number may be added to (or subtracted from) both sides of an inequality without changing the sign of inequality.
Rule 2 :
Both sides of an inequality can be multiplied (or divided) both by the same positive real number without changing the sign of inequality. However, the sign of inequality is revered when both sides of an inequality are multiplied or divided by the negative number.
Rule 3 :
Any term of an inequality may be taken to the other side with its sign changed without affecting sings of inequality.
Example :
Solve the following linear inequality.
2x - 4 ≤ 0
Solution :
2x - 4 ≤ 0
Add 4 to each side.
2x - 4 + 4 ≤ 0 + 4
2x ≤ 4
Divide each side by 2.
x ≤ 2
x ≤ 2
By graphing this in the number line, we can split this as two intervals. (-∞, 2] and [2, ∞).

Now we need to select one of the values from the above intervals and apply those values instead of x in the given question 2x - 4 ≤ 0.
The values from which interval makes the given inequality true is the solution set.
|
(-∞, 2] Let x = 0 2(0) - 4 ≤ 0 - 4 ≤ 0 True |
[2, ∞) Let x = 3 2(3) - 4 ≤ 0 6 - 4 ≤ 0 2 ≤ 0 False |
Therefore, (-∞, 2] is the solution set.
Linear Inequalities in Two Variables
Let a, b, c be real numbers.
Then, the equation ax + by + x = 0 is called a linear equation in two variables.
Whereas the inequalities
ax + by < c
ax + by ≤ c
ax + by > c
ax + by ≥ c
are known as linear inequalities in two variables.
Solving Linear Inequalities in Two Variables
Step 1 :
Convert the given inequality, say ax + by ≤ c, into the equation ax + by = c which represents a straight line in xy-plane.
Step 2 :
Put y = 0 in order to find the x-intercept and similarly put x = 0 to find y-intercept. Now draw the straight by using these intercepts.
Step 3 :
Choose a point and substitute its coordinates in the inequality, if the inequality is satisfied, then shade the portion of the plane contains the chosen point, otherwise shade the portion which does not contain the desired solution set.
Example 1 :
Solve the following inequality graphically
2x - y ≥ 1
Solution :
Consider the linear inequality as if it were a linear equation
2x - y = 1 -----(1)
Find x-intercept :
Substitute 0 for y in (1)
(1)-----> 2x - 0 = 1
2x = 1
Divide each side by 2.
x = 0.5
So, x-intercept is (0.5, 0)
Find y-intercept :
Substitute 0 for x in (1)
(1)-----> 2(0) - y = 1
- y = 1
Multiply each side by (-1).
y = - 1
So, y-intercept is (0, -1).
Using the x-intercept (0.5, 0) and y-intercept (0, -1), we can draw a straight as shown below.
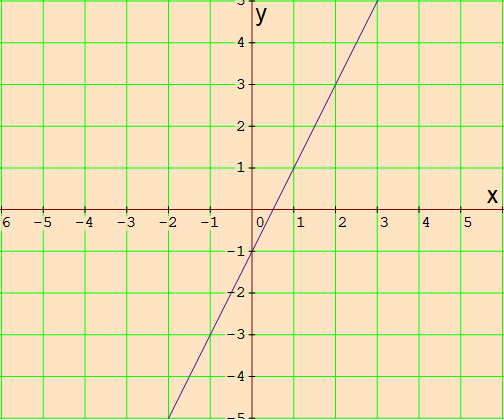
Now we need to take a point on either sides of the line shown above.
Take the two points (-2, 3) and and (2, -2).
Case 1 :
Substitute the point (-2, 3) into the inequality.
2(-2) - 3 ≥ 1 ?
- 4 - 3 ≥ 1 ?
- 7 ≥ 1 ?
- 7 can never be greater than 1
So, the above statement is false.
Hence, the point (-2, 3) does not satisfy the inequality.
Case 2 :
Substitute the point (2, -2) into the inequality.
2(2) - (-2) ≥ 1 ?
4 + 2 ≥ 1 ?
6 ≥ 1 ?
6 is greater than 1
So, the above statement is true.
Hence, the point (-2, 2) satisfies the inequality.
Shade the Solution Region :
Now, we have to shade the region from where the point (2, -2) has been taken.
That is the solution region.
The solution region is shown in the graph below.

Example 2 :
The area of the rectangle is greater than 60 square feet. Write and solve an inequality to find the possible values of x.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 06, 26 04:54 AM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

