THE MEAN VALUE THEOREM

Before proving this theorem, we can see that it is reasonable by interpreting it geometrically.

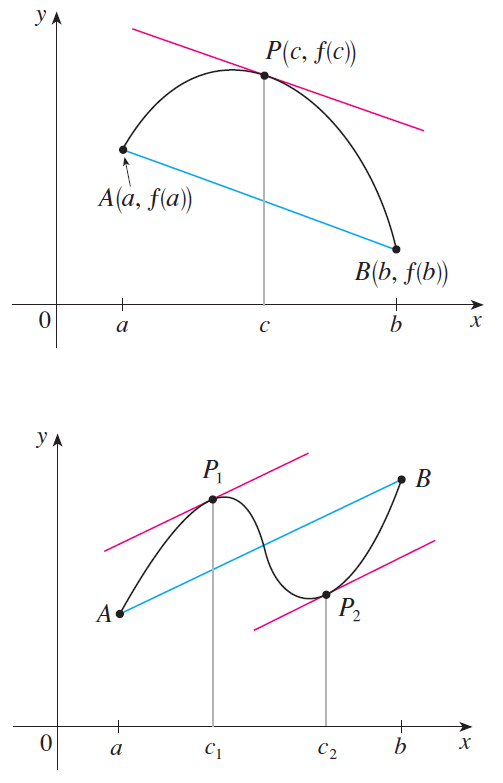
The above picture shows the points

A(a, f(a)) and B(b, f(b))

on the graphs of two differentiable functions. The slope of the secant line AB is

which is the same expression as on the right side of (1). Since f'(c) is the slope of the tangent line at the point 

(c, f(c))

the Mean Value Theorem, in the form given by (1), says that there is at least one point

P(c, f(c))

on the graph where the slope of the tangent line is the same as the slope of the secant line AB. In other words, there is a point P where the tangent line is parallel to the secant line AB. (Imagine a line far away that stays parallel to AB while moving toward AB until it touches the graph for the first time.)

Solved Problems

In each case, find the values of c that satisfy the Mean Value Theorem.

Problem 1 :

f(x) = 2x² - 3x + 1, [0, 2]

Solution :

(i) f(x) is defined and continuous on [0, 2].

f(x) = 2x² - 3x + 1

f'(x) = 4x - 3

(ii) f(x) is differentiable on the interval (0, 2).

The given function satisfies both the hypotheses of the Mean Value theorem.

Then, we have

4c - 3 = 1

4c = 4

c = 1 ∈ (0, 2)

Problem 2 :

f(x) = x³ - 3x + 2, [-2, 2]

Solution :

(i) f(x) is defined and continuous on [-2, 2].

f(x) = x³ - 3x + 2

f'(x) = 3x² - 3

(ii) f(x) is differentiable on the interval (-2, 2).

The given function satisfies both the hypotheses of the Mean Value theorem.

Then, we have

Problem 3 :

Find the number c that satisfies the conclusion of the Mean Value Theorem on the given interval. Graph the function, the secant line through the endpoints, and the tangent line at (c, f(c)). Are the secant line and the tangent line parallel?

(a) f(x) = √x,  [0, 4]

(b) f(x) = e^-x, [0, 2]

Solution (a) :

f(x) = √x,  [0, 4]

(i) f(x) is defined and continuous on [0, 4].

(ii) f(x) is differentiable on the interval (0, 4).

The given function satisfies both the hypotheses of the Mean Value theorem.

Then, we have

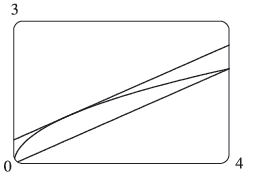
Yes, the secant line and the tangent line parallel.

Solution (b) :

f(x) = e^-x, [0, 2]

(i) f(x) is defined and continuous on [0, 2].

f(x) = e^-x

f'(x) = e^-x(-1)

f'(x) = -e^-x

(ii) f(x) is differentiable on the interval (0, 2).

The given function satisfies both the hypotheses of the Mean Value theorem.

Then, we have

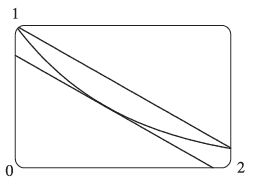
Yes, the secant line and the tangent line parallel.

Problem 4 :

The graph of a function f is shown. Verify that f satisfies the hypotheses of Rolle’s Theorem on the interval [0, 8]. Then estimate the value(s) of c that satisfy the  conclusion of Rolle’s Theorem on that interval.

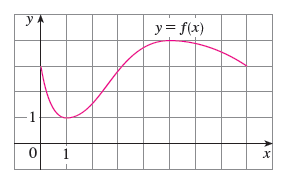
Solution :

(i) f is continuous on the closed interval [0, 8].

(ii) f is differentiable on the open interval (0, 8).

(iii) f(0) = 3 and f(8) = 3.

f(0) = f(3)

Thus, f stratifies the hypotheses of Rolle’s Theorem. The numbers c = 1 and c = 5 satisfy the conclusion of Rolle’s Theorem.

Because, f'(1) = f'(5) = 0.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.