THE MEAN VALUE THEOREM WORKSHEET

In each case, find the values of c that satisfies the Mean Value Theorem.

Problem 1 :

f(x) = x³, [-2, 2]

Problem 2 :

f(x) = 1 - x², [0, 3]

Problem 3 :

Problem 4 :

f(x) = 2x³ + x² - x - 1, [0, 2]

Problem 5 :

Problem 6 :

f(x) = x³ - 5x² - 3x, [1, 3]

Problem 7 :

A cylindrical hole 4 mm in diameter and 12 mm deep in a metal block is rebored to increase the diameter to 4.12 mm. Using the Mean Value Theorem to estimate the amount of metal removed.

Problem 8 :

Suppose that f(0) = -3 and f'(x) ≤ 5 for all values of x, how large can f(2) possibly be?

Answers

1. Answer :

f(x) = x³, [-2, 2]

(i) f(x) is defined and continuous on [-2, 2].

f(x) = x³

f'(x) = 3x²

(ii) f(x) is differentiable on the interval (-2, 2).

The given function satisfies both the hypotheses of the Mean Value theorem.

Then, we have

2. Answer :

f(x) = 1 - x², [0, 3]

(i) f(x) is defined and continuous on [0, 3].

f(x) = 1 - x²

f'(x) = -2x

(ii) f(x) is differentiable on (0, 3).

The given function satisfies both the hypotheses of the Mean Value theorem.

Then, we have

3. Answer :

(i) f(x) is defined and continuous on [1, 2].

(ii) f(x) is differentiable on (1, 2).

The given function satisfies both the hypotheses of the Mean Value theorem.

Then, we have

Therefore,

4. Answer :

f(x) = 2x³ + x² - x - 1, [0, 2]

(i) f(x) is defined and continuous on [0, 2].

f(x) = 2x³ + x² - x - 1

f'(x) = 6x² + 2x - 1

(ii) f(x) is differentiable (0, 2).

The given function satisfies both the hypotheses of the Mean Value theorem.

Then, we have

Therefore,

5. Answer :

(i) f(x) is defined and continuous on [-2, 2].

f'(x) is undefined when x = 0 ∈ (-2, 2)

(ii) f(x) is not differentiable on (-2, 2).

The given function does satisfy the second hypothesis of the Mean Value theorem.

So, the Mean Value Theorem does not hold for the given function.

6. Answer :

f(x) = x³ - 5x² - 3x, [1, 3]

(i) f(x) is defined and continuous on [1, 3].

f(x) = x³ - 5x² - 3x

f(x) = 3x² - 10x - 3

(ii) f(x) is differentiable on (1, 3).

The given function satisfies both the hypotheses of the Mean Value theorem.

Then, we have

7. Answer :

Formula to find voilume of a cylinder :

V = πr²h

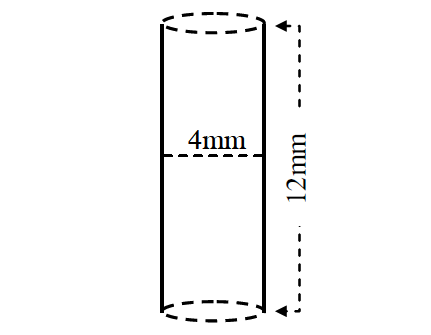
The volume of cylindrical hole of radius x mm and depth 12 mm is given by

V = f(x) = πx²(12)

f(x) = 12πx² ----(1)

Since the diameter is increased from 4 mm to 4.12 mm, the restriction we have for the radius x is

2 ≤ x ≤ 2.06  or  x ∈ [2, 2.06]

(i) f(x) is defined and continuous on [2, 2.06].

f(x) = 12πx²

f'(x) = 12π(2x)

f'(x) = 24πx

(ii) f(x) is differentiable on (2, 2.06).

We have to estimate the following.

f(2.06) - f(2)

By the Mean Value Theorem, we have

f(2.06) - f(2) = 24πc(0.06)

f(2.06) - f(2) = 1.44πc

Since c ∈ (2, 2.06), we can take c = 2.01.

f(2.06) - f(2) = 1.44π(2.01)

f(2.06) - f(2) = 2.89π cubic mm.

Note :

Any suitable c between 2 and 2.06 other than 2.01 also will give other estimates.

8. Answer :

Since by hypothesis f is differentiable, f is continuous everywhere. We can apply the Mean Value Theorem on the interval [0, 2]. There exist atleast one c ∈ (0, 2) such that

f(2) - f(0) = f'(c)(2 - 0)

f(2) - (-3) = 2f'(c)

f(2) + 3 = 2f'(c)

f(2) = 2f'(c) - 3

Given that f'(x) ≤ 5 for all x. In particular we know that

f'(c) ≤ 5

Multiply both sides by 2.

2f'(c) ≤ 10

Subtract 3 from both sides.

2f'(c) - 3 ≤ 10 - 3

f(2) ≤ 7

Therefor, the largest possible value of f(2) is 7.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.