SIMPLIFYING EXPRESSION OF SURDS USING BASIC OPERATIONS

Question 1 :

Simplify the following using addition and subtraction properties of surds:

(i) 5 √3 + 18√3 − 2√3

Solution :

=  5√3 + 18√3 − 2√3

In the given expression, the radical terms are having same index. So, we have easily combine them by factoring √3.

  =  (5 + 18 - 2) √3

  =  21√3

(ii)  4³√5 +2³√5 -3³√5

Solution :

  =  4∛5 + 2 ∛5 −3∛5

In the given expression, the radical terms are having same index. So, we have easily combine them by factoring ∛5.

  =  (4 + 2 - 3) ∛5

  =  3∛5

(iii) 3 √75 + 5 √48 − √243

Solution :

3 √75 + 5 √48 − √243

3 √75  =   3 √(5 ⋅ 5 ⋅ 3)  =  15√3

5 √48  =  5 √(4 ⋅ 4 ⋅ 3)  =  20√3

 √243  =   √(3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3)  =  9√3

  =  (15 + 20 - 9) √3

=  26√3

(iv) 5³√40 + 2³√625 - 3³√320

Solution :

  =  5³√40 + 2³√625 −3³√320

5³√40  =  5³√(2 ⋅ 2 ⋅ 2 ⋅ 5)  =  10³√5

2³√625  =  2³√(5 ⋅ 5 ⋅ 5 ⋅ 5)  =  (2 ⋅ 5)³√5  =  10³√5 

3³√320  =  3³√(2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 5)  =  12³√5

  =  (10 + 10 - 12)³√5 

  =  8³√5 

Question 2 :

Simplify the following using multiplication and division properties of surds :

(i) √3 ⋅ √5 ⋅ √2

Solution :

√3 ⋅ √5 ⋅ √2  =  √(3 ⋅ 5 ⋅ 2)  =  √30

(ii)  √35 ÷ 7

Solution :

√(35/7)  =  √5

(iii) 3³√27 ⋅ 3³√8 ⋅ 3³√125

Solution :

=  3³√27 ⋅ 3³√8 ⋅ 3³√125

  =  27³√(27 ⋅ 8 ⋅ 125)

  =  27³√(3 ⋅ 3 ⋅ 3 ⋅ 2⋅ 2 ⋅ 2 ⋅ 5 ⋅ 5 ⋅ 5)

=  27(3 ⋅ 2 ⋅ 5)

  =  27(30)

  =  810

(iv) (7√a − 5√b)(7√a  + 5√b)

Solution :

Using algebraic identity

(7√a − 5√b) (7√a  + 5√b)  =  (7√a)² - (5√b)²

  =  49a - 25b

(v)

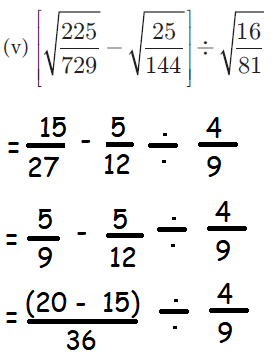
  =  (5/36) x (9/4)

  =  5/16

Question 3 :

If √2 = 1.414, √3 = 1.732, √5 = 2.236, √10 = 3.162 , then find the values of the following correct to 3 places of decimals.

(i)  √40 - √20

Solution :

√40  =  √(2 ⋅ 2 ⋅ 2 ⋅ 5)  =  2√10  = 2(3.162)  =  6.324

√20  =  √(2 ⋅ 2 ⋅ 5)  =  2√5  = 2(2.236)  =  4.472

  =  6.324 - 4.472

  =  1.852

(ii)  √300 + √90 - √8

Solution :

√300  =  √(10 ⋅ 10 ⋅ 3)  =  10√3  =  10(3.162)  =  31.62

√90  =  √(3 ⋅ 3 ⋅ 10)  =  3√10  =  3(3.162)  =  9.486

√8  =  √(2 ⋅ 2 ⋅ 2)  =  2√2  =  2(1.414)  =  2.828

  =  31.62 + 9.486 - 2.828

  =  38.278

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.