SIMPLIFYING COMPLEX FRACTIONS WORKSHEET

Problems 1-4 : Simplify using method I.

Problem 1 :

(2x/27y²)/(6x²/9)

Problem 2 : 

(x/y + 1)/(1 - y/x)

Problem 3 : 

[x/y - y/x] / [1/y² - 1/x²]

Problem 4 : 

[(1 + x²)^1/2 - x²/(1 + x²)^1/2] / (1 + x²)

Problems 5-8 : Simplify using method II.

Problem 5 : 

(y/6x²) / (3/4y²)

Problem 6 : 

[5x/(x + 2)]/[10/(x - 2)]

Problem 7 : 

[x/y² + 1/y] / [y/x² + 1/x]

Problem 8 : 

(x - y/3x) / (y + 1/9x²)

Problem 9 : 

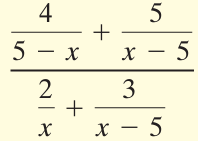
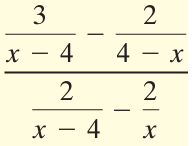
Problem 10 : 

Problem 11 : 

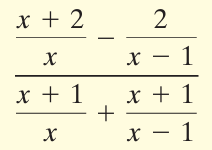
Detailed Answer Key

1. Answer : 

=  (2x/27y²)/(6x²/9)

The numerator of the compound fraction is already a single fraction, and so is the denominator.

Invert the the fraction in denominator and multiply.

=  (2x/27y²) ⋅ (9/6x²)

=  (2x ⋅ 9) / (6x² ⋅ 27y²)

Cancel common factors. 

=  1 / (3x ⋅ 3y²)

=  1/9xy²

2. Answer : 

=  (x/y + 1)/(1 - y/x)

We combine the terms in the numerator into a single fraction and do the same in the denominator. Then we invert and multiply.

=  [(x + y)/y]/[(x - y)/x]

Invert the the fraction in denominator and multiply.

=  [(x + y)/y)] ⋅ [x/(x - y)]

=  [x(x + y)] / [y(x - y)]

3. Answer : 

=  [x/y - y/x] / [1/y² - 1/x²]

We combine the terms in the numerator into a single fraction and do the same in the denominator. Then we invert and multiply.

=  [(x² - y²)/xy] / [(x² - y²)/x²y²]

Invert the the fraction in denominator and multiply.

=  [(x² - y²)/xy] ⋅ [x²y²/(x² - y²)]

=  [(x² - y²)x²y²] / [xy(x² - y²)]

Cancel common factors. 

=  xy

4. Answer : 

=  [(1 + x²)^1/2 - x²/(1 + x²)^1/2] / (1 + x²)

We combine the terms in the numerator into a single fraction and do the same in the denominator. Then we invert and multiply.

=  [{(1 + x²) - x²}/(1 + x²)^1/2] / (1 + x²)

=  [(1 + x² - x²)/(1 + x²)^1/2] / (1 + x²)

=  [1/(1 + x²)^1/2] / (1 + x²)

Invert the the fraction in denominator and multiply.

=  [1/(1 + x²)^1/2] ⋅ [1/(1 + x²)]

=  1/[(1 + x²)^1/2(1 + x²)]

=  1/(1 + x²)^{1/2 + 1}

=  1/(1 + x²)^3/2

5. Answer : 

=  (y/6x²) / (3/4y²)

The least common denominator of the fractions in both numerator and denominator is 12x²y².

Multiply numerator and denominator by the LCD.

=  (y/6x²)(12x²y²) / (3/4y²)(12x²y²)

Simplify. 

=  2y³/9x²

6. Answer : 

=  [5x/(x + 2)]/[10/(x - 2)]

The least common denominator of the fractions in both numerator and denominator is (x + 2)(x - 2). 

Multiply numerator and denominator by the LCD.

=  [5x/(x + 2)](x + 2)(x - 2) / [10/(x - 2)](x + 2)(x - 2)

Simplify.

=  [5x(x - 2)]/[10(x + 2)]

=  x(x - 2)/2(x + 2)

7. Answer : 

=  [x/y² + 1/y] / [y/x² + 1/x]

The least common denominator of the fractions in both numerator and denominator is x²y². 

Multiply numerator and denominator by the LCD.

=  [x/y² + 1/y](x²y²) / [y/x² + 1/x](x²y²)

Use the distributive property.

=  [x/y² ⋅ x²y² + 1/y ⋅ x²y²] / [y/x² ⋅ x²y² + 1/x ⋅ x²y²]

Simplify. 

=  [x³ + x²y]/[y³ + xy²]

Factor. 

=  [x²(x + y)]/[y²(y + x)]

=  x²/y²

8. Answer : 

=  (x - y/3x) / (y + 1/9x²)

The least common denominator of the fractions in both numerator and denominator is 18x².

Multiply numerator and denominator by the LCD.

=  (x - y/3x)(18x²) / (y + 1/9x²)(18x²)

Use the distributive property.

=  (x ⋅ 18x² - y/3x ⋅ 18x²) / (y ⋅ 18x² + 1/9x² ⋅ 18x²)

Simplify. 

=  (18x³ - 6xy)/(18x²y + 2)

Factor. 

=  [2x(9x² - 3y)]/[2(9x²y + 1)]

=  x(9x² - 3y)]/(9x²y + 1)

9. Answer : 

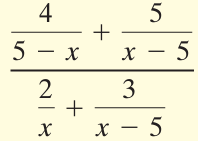
Simplifying numerator :

= 4/(5 - x) + 5/(x - 5)

= -4/(x - 5) + 5/(5 - x)

= (-4 + 5)/(x - 5)

= 1/(x - 5)

Simplifying denominator :

= 2/x + 3/(x - 5)

= [2(x - 5) + 3x] / (x - 5)

= [2x - 10 + 3x] / (x - 5)

= [5x - 10] / (x - 5)

= 5(x - 2) / (x - 5)

Dividing the numerator and denominator, we get

=  [1/(x - 5)] ÷ [5(x - 2) / (x - 5)]

=  [1/(x - 5)] x [(x - 5) / 5(x - 2)]

= 1/5(x - 2)

10. Answer : 

Simplifying numerator :

= 3/(x - 4) - 2/(4 - x)

= 3/(x - 4) + 2/(x - 4)

= (3 + 2) / (x - 4)

= 5/(x - 4)

Simplifying denominator :

= 2/(x - 4) - (2/x)

= [2x - 2(x - 4)]/x(x - 4)

= [2x - 2x + 8]/x(x - 4)

= 8/x(x - 4)

Dividing the numerator and denominator, we get

= [5/(x - 4)] ÷ [8/x(x - 4)]

= [5/(x - 4)] x [x(x - 4)/8]

 5/8x

11. Answer : 

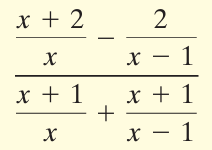
Simplifying numerator :

= (x + 2)/x - 2/(x - 1)

Least common multiple for the denominators are x(x - 1)

= [(x + 2)(x - 1) - 2x]/x(x - 1)

= [(x² - x + 2x - 2) - 2x]/x(x - 1)

= [(x² + x - 2) - 2x]/x(x - 1)

= (x² + x - 2 - 2x)/x(x - 1)

= (x² - x - 2)/x(x - 1)

Simplifying denominator :

= (x + 1)/x - [(x + 1)/(x - 1)]

= [(x + 1)(x - 1) - x(x + 1)]/x(x - 1)

= [(x² - 1) - (x² + x)]/x(x - 1)

= [x² - 1 - x² - x]/x(x - 1)

= -(x + 1) / x(x - 1)

Dividing the numerator and denominator, we get

= (x² - x - 2)/x(x - 1) ÷ [-(x + 1) / x(x - 1)]

= [(x² - x - 2)/x(x - 1)] x [-x(x - 1)/(x + 1)]

= -(x² - x - 2)/(x + 1)

= -(x² - 2x + x - 2)/(x + 1)

= -(x - 2)(x + 1)/(x + 1)

= -(x - 2)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.