SIMPLE INTEREST EXAMPLES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Example 1 :
Lily wants to have an interest income of $3,000 a year. How much must she invest for one year at 8%?
Solution :
Formula for simple interest is
I = Prt
Here, I = 3000, t = 1, r = 8%.
Let us plug these values in the above formula
3000 = P ⋅ 8/100 ⋅ 1
3000 = P ⋅ 2/25
Multiply both sides by 25/2.
25/2 ⋅ 3000 = P
37500 = P
So, Lily she must invest $37,500.
Example 2 :
Alex owes the bank some money at 4% per year. After half a year, he paid $45 as interest. How much money does she owe the bank?
Solution :
Formula for simple interest is
I = Prt
Here, I = 45, t = 1/2, r = 4%.
Let us plug these values in the above formula.
45 = P ⋅ 4/100 ⋅ 1/2
45 = P ⋅ 1/50
Multiply both sides by 50.
50 ⋅ 45 = P
2250 = P
So, Lily she must invest $2,250.
Example 3 :
How long does it take a principal of $25,000 at a simple interest rate of 5% to become $30,000?
Solution :
Interest earned (I) = Amount - Principal
I = $30,000 - $25,000
I = $5,000
Formula for simple interest is
I = Prt
Here, P = 25000, I = 5000, r = 5%.
Substitute these values in the above formula.
5000 = 25000 ⋅ 5/100 ⋅ t
5000 = 1250t
Divide both sides by 1250.
4 = t
So, it will take 4 years for the principal of $25,000 at a simple interest rate of 5% to become $30,000.
Example 4 :
$45,000 is deposited into a savings account. After one year, 4 months and 20 days it totals $52,500. Calculate the simple interest rate for this account.
Solution :
Given : Time period is 1 year, 4 months
1 year, 4 months = 1⁴⁄₁₂ years
1 year, 4 months = 1⅓ years
1 year, 4 months = 4/3 years
So, the time period is 4/3 years.
Interest earned (I) = Amount - Principal
I = $52,500 - $45,000
I = $7,500
Formula for simple interest is
I = Prt
Here, P = 45000, I = 7500, t = 4/3.
Let us plug these values in the above formula
7500 = 45000 ⋅ r ⋅ 4/3
7500 = 60000 ⋅ r
Divide both sides by 60000.
7500/60000 = r
0.125 = r
To convert the decimal 0.125 into percentage, multiply it by 100.
12.5% = r
So, the simple interest rate for the given account is 12.5%.
Example 5 :
Mr. Berman put his savings into two accounts, which pay 6% and 9% annual rate. If he invested a total of $22,000 and received $1440 as interest after one year. How much did he put into each account?
Solution :
Let x be the amount invested at 6% annual rate.
Then, the amount invested at 9% annual rate is
= 22000 - x
Given : Total interest received after one year is $1440.
So, we have
Interest at 6% rate + Interest at 9% rate = 1440
x ⋅ 6/100 ⋅ 1 + (22000 - x) ⋅ 9/100 ⋅ 1 = 1440
0.06x + (22000 - x)0.09 = 1440
0.06x + 1980 - 0.09x = 1440
1980 - 0.03x = 1440
1980 - 1440 = 0.03x
540 = 0.03x
Divide both sides by 0.03.
540/0.03 = x
54000/3 = x
18000 = x
And also,
22000 - x = 22000 - 18000
24000 - x = 4000
So, the amount invested at 6% rate is $18,000 and at 9% rate is $4,000.
Example 6 :
Mr. George invests his inheritance of $30,000 in two different accounts which pay 7% and 9% annual interest. It is given that he gets more interest at 9% rate than 7% rate. After one year, if the difference between the interest received in two accounts is $140, find the amount invested in each account.
Solution :
Let x be the amount invested at 7% annual rate.
Then, the amount invested at 9% annual rate is
= 30000 - x
After one year, interest earned at 7% rate is
= x ⋅ 7/100 ⋅ 1
= 0.07x ---(1)
After one year, interest earned at 9% rate is
= (30000 - x) ⋅ 9/100 ⋅ 1
= (30000 - x) ⋅ 0.09
= 2700 - 0.09x ----(2)
Given : Difference between the interest received in two accounts is $140 and also interest received at 9% is more than 7%.
That is, (2) > (1).
So, we have
(2) - (1) = 140
2700 - 0.09x - 0.07x = 140
2700 - 0.16x = 140
2700 - 140 = 0.16x
2560 = 0.16x
Divide both sides by 0.16.
2560/0.16 = x
256000/16 = x
16000 = x
And also,
30000 - x = 30000 - 16000
30000 - x = 14000
So, the amount invested at 7% rate is $16,000 and at 9% rate is $14,000.
Example 7 :
In simple interest, a sum of money doubles itself in 10 years. Find the number of years it will take to triple itself.
Solution :
Let P be the sum of money invested.
Given : Sum of money doubles itself in 10 years.
Then, P will become 2P in 10 years.
Now we can calculate interest for ten years as given below.
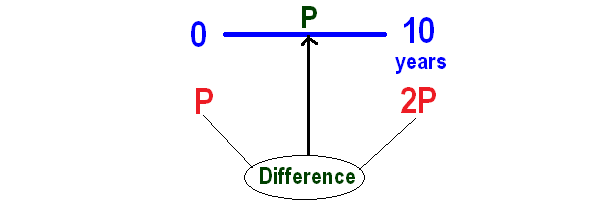
From the above calculation, P is the interest for the first 10 years.
In simple interest, interest earned will be same for every year.
So, interest earned in the next 10 years also will be P.
It has been explained below.
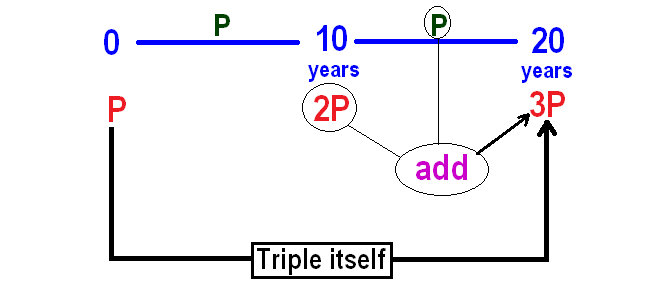
So, it will take 20 years for the principal to become triple itself.
Example 8 :
In simple interest, a sum of money amounts to $ 6200 in 2 years and $ 7400 in 3 years. Find the principal.
Solution :
At the end of 2 years, we get $6200.
At the end of 3 years, we get $7400.
From these two information, we can get the interest earned in the 3rd year as given below.
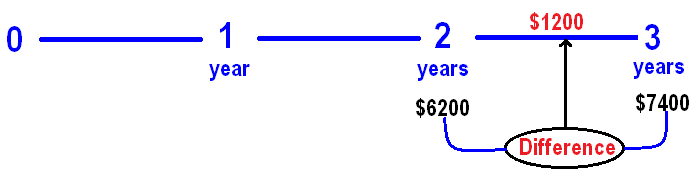
In simple interest, interest will be same for every year.
Based on this, we can calculate the principal as given below.
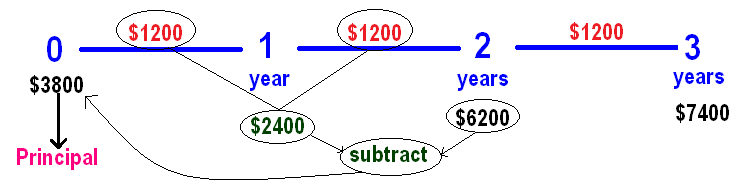
So, the principal is $3800.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Solving the HARDEST SAT Math Questions ONLY using Desmos
Dec 31, 25 05:53 AM
Solving the HARDEST SAT Math Questions ONLY using Desmos -
Times Table Shortcuts
Dec 30, 25 07:14 PM
Times Table Shortcuts - Concept - Examples -
10 Hard SAT Math Questions (Part - 42)
Dec 30, 25 05:52 AM
10 Hard SAT Math Questions (Part - 42)
