SEGMENTS AND THEIR MEASURES

In geometry, rules that are accepted without proof are called postulates or axioms. Rules that  are proved are called theorems. In this section, we are going to study two postulates about the lengths of segments. 

Postulate 1 (Ruler Postulate)

The points on a line can be matched one to one with real numbers. The real number that corresponds to a point is the coordinate of the point. 

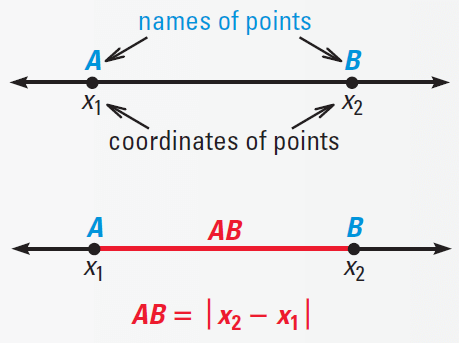
The distance between points A and B, written as AB, is the absolute value of the difference between the coordinates of A and B. 

AB is also called the length AB. 

Example (Postulate 1) :

Measure the length of the segment to the nearest millimeter. 

Solution :

Use a metric ruler. 

Align one mark of the ruler with A, then estimate the coordinate of B. 

For example, if we align A with 3, B appears to align with 5.5 as shown below.  

Now, we have

AB  =  |5.5 - 3|  =  |2.5|  =  2.5

The distance between A and B is 2.5 cm.

Note :

It does not matter, how we place the ruler.

For example, if the ruler in the above example is placed such that A is aligned with 4, then B aligns with 6.5. The difference in the coordinates is same.

That is,

AB  =  |6.5 - 4|  =  |2.5|  =  2.5

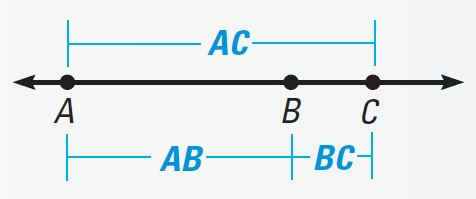
Postulate 2 (Segment Addition Postulate)

If B is between A and C, then, we have

AB + BC  =  AC.

(or)

If AB + BC  =  AC, then B is between A and C. 

It has been illustrated in the picture given below.

Example (Postulate 2) :

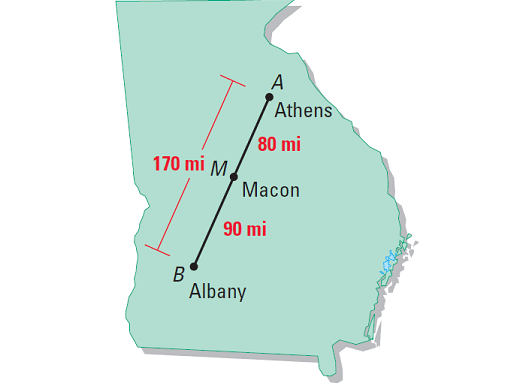
Use the map to find the distances between the three cities that lie on a line.

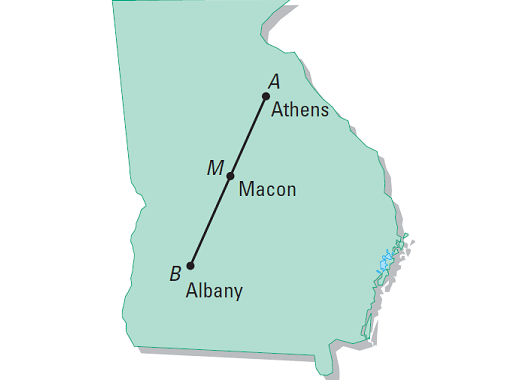
Solution :

Using the scale on the map, we can estimate that the difference between Athens and Macon is

AM  =  80 miles

The distance between Macon and Albany is

MB  =  90 miles

It has been explained in the picture given below.

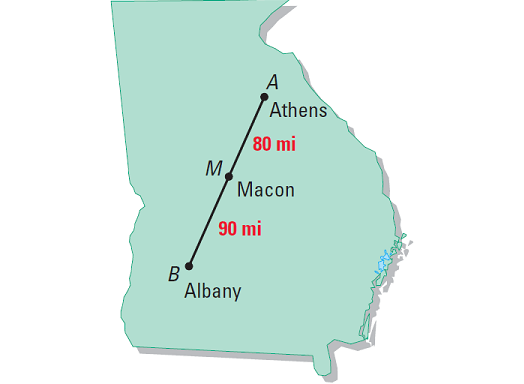
Knowing that Athens, Macon and Albany lie on the same line, we can use the Segment Addition Postulate to conclude that the distance between Athens and Albany is

AB  =  AM + MB

AB  =  80 + 90

AB  =  170 miles

It has been explained in the picture given below.

Reflect (Segment Addition Postulate)

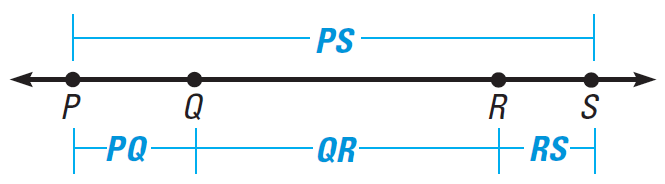
The Segment Addition Postulate can be generalized to three or more segments, as long as the segments lie on a line. If P, Q, R and S lie on a line as shown, then

PS  =  PQ + QR + RS

It has been explained in the picture given below.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.