SECTION FORMULA WORKSHEET WITH ANSWERS

(1) Find the coordinates of the point which divides the join of (-1,7) and (4,-3) in the ratio 2 : 3.     Solution

(2) Find the coordinates of the points of trisection of the line segment joining (4,-1) and (-2,-3).      Solution

(3) To conduct sports day activity, in your rectangular shaped school ground ABCD, lines have been drawn which chalk powder at a distance of 1 m each 100 flower pots have been placed at a distance of 1 m from each other along AD,as shown in figure. 

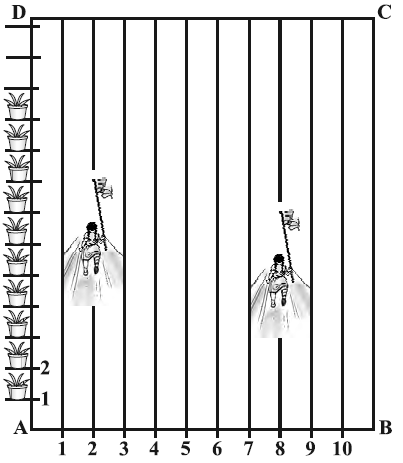
Niharika runs ¼ th the distance AD on the second line and posts a green flag. Preet runs 1/5th the distance AD on the eight line and posts a red flag. What  is between both the flags?

If Rashmi has to post a blue flag exactly halfway between the line segment joining the two flags,where should she post her flag?      Solution

(4)  The point which divides the line segment joining the points (7, –6) and (3, 4) in ratio 1 : 2 internally lies in the

(A) I quadrant      (B) II quadrant

(C) III quadrant    (D) IV quadrant

Solution

(5)  Point P divides  the line segment joining hte points A(2, 1) and B(5, -8) such that AP : PB = 1 : 3 if P lies on the line 2x - y + k = 0, then find the value of k.

Solution

(6)  The fourth vertex D of a parallelogram ABCD whose three vertices are A (–2, 3), B (6, 7) and C (8, 3) is

(A) (0, 1)   (B) (0, –1)   (C) (–1, 0)    (D) (1, 0)

Solution

1)  Find the ratio in which the line segment joining the points (-3, 10) and (6, -8) is divided by (-1, 6).

Solution

2)  Find the ratio in which the line segment joining A (1, -5) and B(-4, 5) is divided by the x axis. Also find the coordinates of the point of division.

Solution

3)  If (1, 2), (4, y) (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y

Solution

4)  Find the ratio in which the line 2x + 3y - 5 = 0 divides the line segment joining the points (8, -9) and (2, 1). Also, find the co-ordinates of the point of division.

Solution

5)  The point P divides the join of (2, 1) and (-3, 6) in the ratio 2 : 3. Does P lie on the line x - 5y + 15 = 0 ?

Solution

1)  Find the coordinates of a point A, where AB is the diameter of a circle whose center is (2, -3) and B(1, 4)

Solution

2)  If A and B are (-2, -2) and (2, -4) respectively, find the coordinates of P such that AP = (3/7) AB and P lies on the line segment AB.

Solution

3)  Find the coordinates of the points which divide the line segment joining A (-2, 2) and B(2, 8) into four equal parts.

Solution

4)  Find the area of a rhombus if its vertices are (3,0) (4,5) (-1,4) and (-2,-1) taken in order.[Hint : Area of rhombus = (1/2) product of its diagonals]

Solution

5)  If P(9a - 2, -b) divide the line segment joining the points A(3a + 1, -3) and B(8a, 5) in the ratio 3 : 1. Find the values of a and b.

Solution

6)  If (a, b) is the midpoint of the line segment joining the points A(10, -6) and B(k, 4) and a - 2b = 18, find the value of k and distance of AB.

Solution

1)  Find the coordinates of the point which divides the line segment joining the points A(4,−3) and B(9, 7) in the ratio 3:2.

Solution

2)  In what ratio does the point P(2,−5) divide the line segment joining A(−3, 5) and B(4, −9).

Solution

3)  Find the coordinates of a point P on the line segment joining A(1, 2) and B(6, 7) in such a way that AP = (2/5) AB.

Solution

4)  If the points A(4, 3) and B(x, 5) are on circle with center O(2, 3), then find the value of x.

Solution

5)  Find the ratio in which the line 2x + 3y = 10 divide the line segment joining the points (1, 2) and (2, 3).

Solution

6)  Determine the ration in which the point P(a, -2) divides the line joining of points A(-4, 3) and B(2, -4). Also find the value of a.

Solution

7)  If the point C(-1, 2) divides internally the line segment joining A(2, 5) and in the ratio 3 : 4. Find the coordinate of B.

Solution

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.