SOLVING WORD PROBLEMS USING SECTION FORMULA

Problem 1 :

Find the coordinates of a point A, where AB is the diameter of a circle whose center is (2, -3) and B(1, 4)

Solution :

Midpoint of the diameter is center

Center  =  (2,-3)

Let the coordinate of point A be (a, b)

Here x₁  =  a, y₁  =  b, x₂  =  1, y₂  =  4 

Midpoint = (x₁ + x₂)/2 , (y₁ + y₂)/2

(a + 1)/2, (b + 4)/2  =  (2, -3)

Equating the coordinates of x and y 

(a + 1)/2  =  2       (b + 4)/2  =  -3

a + 1  =  4        b + 4  =  -6

a  =  4 - 1         b  =  -6 -4

a  =  3           b  =  -10

Therefore the coordinate of A is (3,-10).

Problem 2 :

If A and B are (-2, -2) and (2, -4) respectively, find the coordinates of P such that AP = (3/7) AB and P lies on the line segment AB.

Solution :

AP  =  (3/7) AB

AP/AB  =  3/7

AB is the line segment P is a point lies on the line segment.

AB  =  AP + PB

7  =  3 + PB

PB  =  4

AP : PB  =  3 : 4

x₁  =  -2, y₁  =  -2, x₂  =  2, y₂  =  -4, m = 3 and n = 4

Coordinates of P

=  [3(2) + 4(-2)]/(3 + 4) , [3(-4) + 4(-2)]/(3 + 4)

=  (6 - 8)/7,(-12 - 8)/7

=  -2/7, -20/7

Problem 3 :

Find the coordinates of the points which divide the line segment joining A (-2, 2) and B(2, 8) into four equal parts.

Solution :

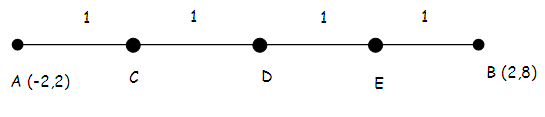
Let "C", "D" and "E" be the points which divides the line segment into four equal parts.

length of AC = 1 unit

length of CD = 1 unit

length of DE = 1 unit

then length of EB is also = 1 unit

So, C divides the line segment in the ratio 1 : 3

x₁  =  -2, y₁  =  2, x₂  =  2, y₂  =  8, m  =  1  and n  =  3

=  [1(2) + 3(-2)]/(1 + 3) , [1(8) + 3(2)]/(1 + 3)

=  (2 - 6)/4, (8 + 6)/4

=  -4/4, 14/4

=  (-1,7/2)

D divides the line segment in the ratio 2 : 2

x₁  =  -2, y₁  =  2, x₂  =  2, y₂  =  8, m  =  2  and n  =  2

=  [2(2) + 2(-2)]/(2 + 2) , [2(8) + 2(2)]/(2 + 2)

=  (4 - 4)/4, (16 + 4)/4

=  0/4, 20/4

=  (0, 5)

E divides the line segment in the ratio 3 : 1

x₁  =  -2, y₁  =  2, x₂  =  2, y₂  =  8, m  =  3  and n  =  1

=  [3(2) + 1(-2)]/(3 + 1) , [3(8) + 1(2)]/(3 + 1)

=  (6 - 2)/4, (24 + 2)/4

=  4/4, 26/4

=  (1, 13/2)

Problem 4 :

Find the area of a rhombus if its vertices are (3,0) (4,5) (-1,4) and (-2,-1) taken in order.[Hint : Area of rhombus = (1/2) product of its diagonals]

Solution :

 Let A(3, 0) B(4, 5) C(-1, 4) and D(-2, -1) are the vertices of the rhombus.

length of diagonal AC =  √(x₂ - x₁)² + (y₂ - y₁)²

x₁  =  3, y₁  =  0,  x₂  =  -1, y₂  =  4

=  √(-1 - 3)² + (4 - 0)²

=  √(-4)² + 4²

=  √16 + 16

  =  √32

x₁  =  4, y₁  =  5,  x₂  =  -2, y₂  =  -1

=  √(-2-4)² + (-1-5)²

=  √(-6)² + (-6)²

=  √36 + 36

=  √72

Area of rhombus = (1/2) x √32 x √72

=  (1/2) ⋅ 4 √2 ⋅ 6√2

=  24 square units. 

Problem 5 :

If P(9a - 2, -b) divide the line segment joining the points A(3a + 1, -3) and B(8a, 5) in the ratio 3 : 1. Find the values of a and b.

Solution :

P is the point divides the line segment joining the points A and B in the ratio 3 : 1.

= [3(8a) + 1(3a + 1)] / (3 + 1), [3(5) + 1(-3)] / (3 + 1)

= [24a + 3a + 1] / 4, (15 - 3) / 4

= [27a + 1] / 4, 12 / 4

= [27a + 1]/4, 3

(27a + 1)/4, 3 = (9a - 2, -b)

So, the value of a is 1 and b is -3.

Problem 6 :

If (a, b) is the midpoint of the line segment joining the points A(10, -6) and B(k, 4) and a - 2b = 18, find the value of k and distance of AB.

Solution :

Midpoint = (10 + k)/2, (-6 + 4)/2

(a, b) = (10 + k)/2, -2/2

(a, b) = (10 + k)/2, -1

Comparing the corresponding terms, we get

(10 + k)/2 = a and b = -1

10 + k = 2a

a = (10 + k)/2

Given that a - 2b = 18

Applying the value of a, we get

[(10 + k)/2] - 2(-1) = 18

[(10 + k)/2] + 2 = 18

(10 + k + 4)/2 = 18

14 + k = 36

k = 36 - 14

k = 22

Distiance between the points A and B

= √(x₂ - x₁)² + (y₂ - y₁)²

A(10, -6) and B(22, 4)

=  √(22 - 10)² + (4 + 6)² 

=  √12² + 10² 

=  √(144 + 10)

=  √154

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.