EXAMPLE PROBLEMS ON SECTION FORMULA

Example 1 :

Find the coordinates of the point which divides the line segments joining (-1, 7) and (4, -3) internally in the ratio 2 : 3.

Solution :

Here x₁  =  -1, y₁  =  7, x₂  =  4 , y₂  =  -3 l = 2  and m = 3.

  =  [2(4) + 3(-1)]/(2+3) , [2(-3) + 3(7)]/(2+3)

  =  (8 - 3)/5, (-6+21)/5

  =  (5/5, 15/5)

  =  (1, 3)

Example 2 :

Find the coordinates of the points of trisection of the line segment joining (4, -1) and (-2, -3).

Solution :

Let "C" and "D" be the points which divides the line segment into three equal parts.

length of AC = 1 unit

length of CD = 1 unit

length of DB = 1 unit

So C divides the line segment in the ratio 1 : 2

Here x₁  =  4, y₁  =  -1, x₂  =  -2, y₂  =  -3, l  =  1  and m = 2.

  =  [1(-2) + 2(4)]/(1+2) , [1(-3) + 2(-1)]/(1+2)

  =  (-2 + 8)/3, (-3-2)/3

  =  6/3, -5/3

  =  (2,-5/3)

So, D divides the line segment in the ratio 2 : 1

Here x₁  =  4, y₁  =  -1, x₂  =  -2 , y₂  =  -3  m = 2  and n = 1

  =  [2(-2) + 1(4)]/(2+1) , [2(-3) + 1(-1)]/(2+1)

  =  (-4 + 4)/3, (-6-1)/3

  =  (0/3, -7/3)

  =  (0,-7/3)

Example 3 :

To conduct sports day activity, in your rectangular shaped school ground ABCD, lines have been drawn which chalk powder at a distance of 1 m each 100 flower pots have been placed at a distance of 1 m from each other along AD, as shown in figure given below.

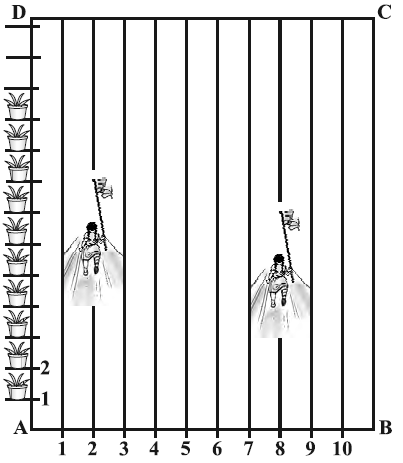
Niharika runs ¼ th the distance AD on the second line and posts a green flag. Preet runs 1/5th the distance AD on the eight line and posts a red flag.

What  is between both the flags? If Rashmi has to post a blue flag exactly halfway between the line segment joining the two flags,where should she post her flag?

Solution :

It can be observed that Naharika posted a green flag at 1/4 th of the distance AD

That is,

(1/4) x 100  = 25 m

from the starting point of the 2nd line.

So, the coordinate of the point is (2, 25)

Preet post red flag at 1/5th of the distance AD.

(1/5) x 100  =  20m

from the starting point of the 8th line.

So, the coordinates of this point R are (8, 20). Distance between these flags.

  =  √(x₂ - x₁)² + (y₂ - y₁)²

  =  √(8 - 2)² + (20 - 25)²

  =  √6² + (-5)²

  =  √36 + 25

  =  √61 m

The point at which Rashmi should post her blue flag is the midpoint of the line joining these points.

 x  =  (8 + 2)/2, y  =  (25 + 20)/2

  =  10/2, 45/2

  =  (5, 22.5)

So, Rashmi should post her flag at 22.5 m on 5^th line. 

Example 4 :

The point which divides the line segment joining the points (7, –6) and (3, 4) in ratio 1 : 2 internally lies in the

(A) I quadrant      (B) II quadrant

(C) III quadrant    (D) IV quadrant

Solution :

= (mx₂ + nx₁)/(m + n), (my₂ + ny₁)/(m + n)

= [1(3) + 2(7)] / (1 + 2), [1(4) + 2(-6)] / (1 + 2)

= (3 + 14)/3, (4 - 12)/3

= (17/3, -8/3)

The required point is in the form of (x, -y), so the required point lies in fourth quadrant.

Example 5 :

Point P divides  the line segment joining hte points A(2, 1) and B(5, -8) such that AP : PB = 1 : 3 if P lies on the line 2x - y + k = 0, then find the value of k.

Solution :

= (mx₂ + nx₁)/(m + n), (my₂ + ny₁)/(m + n)

AP : PB = 1 : 3

= [1(5) + 3(2)]/(1 + 3), [1(-8) + 3(1)]/(1 + 3)

= (5 + 6)/4, (-8 + 3)/4

= (11/4, -5/4)

The point lies on the line 2x - y + k = 0

2(11/4) - (-5/4) + k = 0

(22/4) + (5/4) + k = 0

(22 + 5 + 4k)/4 = 0

27 + 4k = 0

4k = -27

k = -27/4

Example 6 :

The fourth vertex D of a parallelogram ABCD whose three vertices are A (–2, 3), B (6, 7) and C (8, 3) is

(A) (0, 1)   (B) (0, –1)   (C) (–1, 0)    (D) (1, 0)

Solution :

In parallelogram, the diaognals will bisect each other.

Let D be the required point (a, b). AC is the diagonal in which E is the point of intersection of the diagonals AC and BD.

Finding the point E :

= (1(8) + 1(-2))/(1 + 1), (1(3) + 1(3))/(1 + 1)

= (8 - 2)/2, (3 + 3)/2

= (6/2, 6/2)

= (3, 3) -------(1)

Finding the vertex D :

= (1(a) + 1(6))/(1 + 1), (1(b) + 1(7))/(1 + 1)

= (a + 6)/2, (b + 7)/2-----(2)

(1) = (2)

D(0, -1). So, option B is correct.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.