REPRESENTING LINEAR INEQUALITIES ON A NUMBER LINE

To represent the given inequalities in the number line, we must know the below rules.

1. If we have the inequality

< (less than) or > (greater than),

we have to use the empty / unfilled circle.

2. If we have the inequality sign 

≤ (less than or equal to) or ≥ (greater than or equal to),

we have to use the filled circle.

To see more examples

Also we must know the meaning of two words "And & Or".

To see more examples

Represent the inequalities on a number line :

Example 1 :

x ≤ 7

Solution :

Let us represent the given inequality in the number line.

x ≤ 7

Since the given inequality x ≤ 7 (less than or equal), so we draw the line left side from 7 with a filled circle on the number line.

Example 2 :

x > 8

Solution :

x > 8

Since the given inequality x > 8 (greater than), so we draw the line right side from 8 with an unfilled circle on the number line.

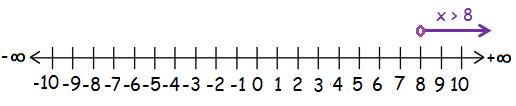
Example 3 :

-8 < x ≤ 10

Solution :

-8 < x ≤ 10

Since the given inequalities -8 < x ≤ 10 (less than and less than or equal), so we draw the line from -8 with an unfilled circle to 10 with a filled circle on the number line.

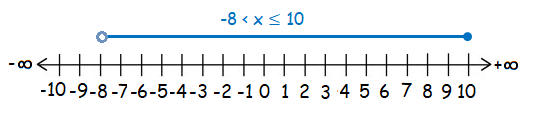
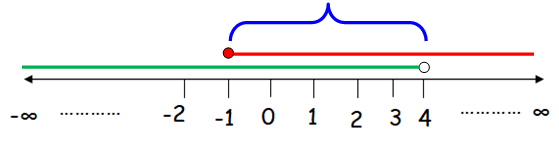
Example 4 :

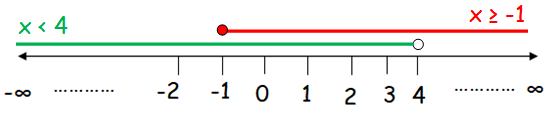
x ≥ −1 and x < 4

Solution :

Given, x ≥ −1 and x < 4 is a compound inequality AND.

Since the first inequality x ≥ −1 (greater than or equal), so we draw the line right side from -1 with a filled circle on the number line.

Since the second inequality x < 4 (less than), so we draw the line left side from 4 with an unfilled circle on the number line.

Now, we have to find the overlapping region(intersection).

Example 5 :

x ≤ -2 or x ≥ 0

Solution :

Given, x ≤ -2 or x ≥ 0 is a compound inequality OR.

Since the first inequality x ≤ -2 (less than or equal), so we draw the line left side from -2 with a filled circle on the number line.

Since the second inequality x ≥ 0(greater than or equal), so we draw the line right side from 0 with a filled circle on the number line.

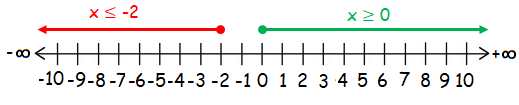
Since we have OR, we combine all the solution of both inequalities.

Example 6 :

Elisa won 40 lollipops playing basketball at the school fair. She gave two to every student in her math class. She has at least 7 lollipops left.

a) Write an inequality to represent the situation. Be sure to define your variable.

b) Solve the inequality to find the maximum number of students in her class

Solution :

Let x be the number of students in her class.

Total number of lollipops = 40

Number of lollipops given = 2

40 - 2x ≥ 7

-2x ≥ 7 - 40

-2x ≥ -33

x ≤ 33/2

x ≤ 16.5

So, approximately 16 students.

Example 7 :

More than 450 students went on a field trip. Ten buses were filled and 5 more students traveled in a car.

a) Write an inequality to represent the situation. Be sure to define your variable.

b) Solve the inequality to find the minimum number of people on each bus.

Solution :

Let x be the number of people in each bus.

10x + 5 > 450

10x > 450 - 5

10x > 445

x > 445/10

x > 44.5

Minimum number of people is 45.

Write an inequality for each graph :

Example 8 :

Solution :

At 0, we have filled circle. 

By observing the shaded portion :

The region is lesser than 0.

Inequality sign to be used :

≤

So, the inequality represented by the graph is x ≤ 0

Example 9 :

Solution :

At 0, we have unfilled circle. 

By observing the shaded portion :

The region is greater than 3.

Inequality sign to be used :

>

So, the inequality represented by the graph is x > 3

Example 10 :

Solve the inequality 

-10 < 6x + 2 ≤ 32

Solution :

-10 < 6x + 2 ≤ 32

Subtracting 2,

-10 - 2 < 6x + 2 - 2 ≤ 32 - 2

-12 < 6x ≤ 30

Dividing by 6, we get

-12/6 < 6x/6 ≤ 30/6

-2 < x ≤ 5

Example 11 :

Solve the inequality 

-4 + 2(p - 8) < -36

Solution :

-4 + 2(p - 8) < -36

Adding 4 on both sides, we get

2(p - 8) < -36 + 4

2(p - 8) < -32

Dividing by 2, we get

(p - 8) < -32/2

(p - 8) < -16

Adding 8 on both sides 

p < -16 + 8

p < -8

Example 12 :

Solve the inequality 

3(6 - 6x) < 4(x - 1)

Solution :

3(6 - 6x) < 4(x - 1)

Distributing 3 and 4, we get

18 - 18x < 4x - 4

-18x - 4x < -4 - 18

-22x < -22

x > -22/(-22)

x > 1

Related pages

• Compound inequalities and or
  
• Solving compound inequalities
  
• How to solve absolute value inequalities on a number line
  
• How to write linear inequalities in slope intercept form
  

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.