HOW TO SOLVE ABSOLUTE VALUE INEQUALITIES ON A NUMBER LINE

Example 1 :

Solve for x :

2|x + 1| - 6 < 7

Graph the solution set in a number line.

Solution :

2|x + 1| - 6  <  7

Add 6 on both sides

2|x + 1|  <  13

Divide by 2 on both sides

|x + 1|  <  13/2

Now we may split this into two branches as shown below. 

So, the solution is

-15/2 < x < 11/2

By graphing the above solution set, we get

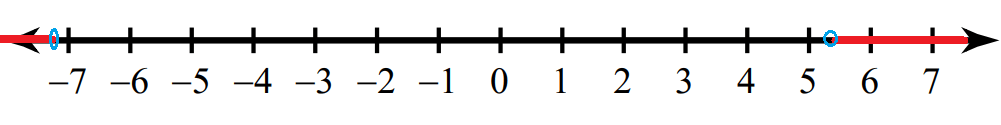
By representing the above graph in solution set, we get

(-∞, -15/2) U (11/2, ∞)

Example 2 :

Solve for x : 

(1/5)|10x - 2|  <  1

Solution :

 (1/5) |10x - 2|  <  1

Multiply each side by 5. 

|10x - 2|  <  5

So, the solution is

-3/10 < x < 7/10.

Example 3 :

Solve for x :

|5x - 12| < -2

Solution :

|5x - 12| < -2

In the right side, we have numerical value -2 and in the left side, we have a absolute value function.

By applying any values to x, we get only positive values on the right side. So the given statement will never become true for any value of x.

Hence, there is no solution for the given inequality.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.