HOW TO REPRESENT THE GIVEN INEQUALITIES IN INTERVAL NOTATION

We may easily represent the given inequalities in interval notation by representing them in the number line.

To graph the given inequalities in the number line, we must know the meaning of two words "And & Or".

AND

A compound inequality containing and is true only if both inequalities are true. Thus, the graph of a compound inequality containing and is the intersection of the graphs of the two inequalities.

In other words, the solution must be a solution of both inequalities.

The intersection can be found by graphing each inequality and then determining where the graphs overlap.

OR

Another type of compound inequality contains the word or. A compound inequality containing or is true if one or more of the inequalities is true. The graph of a compound inequality containing or is the of the graphs of the two inequalities.

In other words, the solution of the compound inequality is a solution of either inequality, not necessarily both. The union can be found by graphing each inequality.

Questions :

Represent the following inequalities in the interval notation:

(i) x ≥ −1 and x < 4

(ii) x ≤ 5 and x ≥ −3

(iii) x < −1 or x < 3

(iv) -2x > 0 or 3x - 4 < 11

Solution (i) :

x ≥ −1 and x < 4

Let us represent each of the given linear inequalities in the number line.

In the first inequality, we have the sign ≥ (greater than or equal). So, we have to use filled circle.

In the second inequality, we have the sign < (less than). So, we have to use unfilled circle.

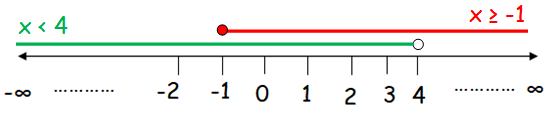
Now, we have to find the overlapping region.

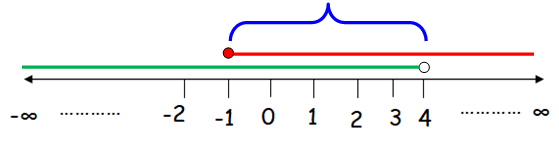
Hence the required interval notation for the given linear inequalities is [-1, 4).

Solution (ii) :

x ≤ 5 and x ≥ −3

Let us represent each of the given linear inequalities in the number line.

Both inequalities are having the signs ≤ (less than or equal) and ≥ (greater than or equal). So, we have to use filled circle.

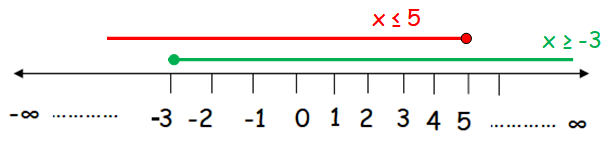
Now, we have to find the overlapping region.

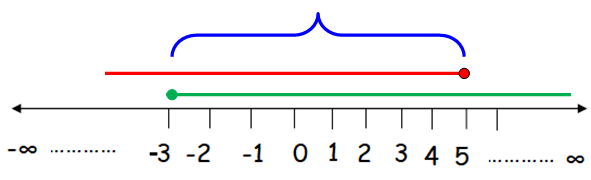
Hence the required interval notation for the given linear inequalities is [-3, 5].

Solution (iii) :

x < −1 or x < 3

Let us represent each of the given linear inequalities in the number line.

Both inequalities are having the signs < (less than). So, we have to use unfilled circle.

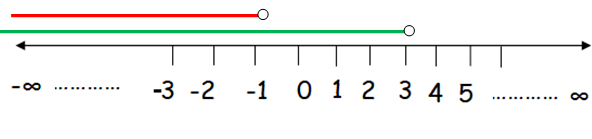
Sine we have "OR", the solution need not to be satisfied by both inequalities.

Hence the required interval notation for the given inequalities is (-∞, 3)

Solution (iv) :

-2x > 0 or 3x - 4 < 11

First let us solve the given inequalities

-2x > 0

x < 0

3x − 4 < 11

Add both sides by 4

3x < 11 + 4

3x < 15

Divide both sides by 3

x < 15/3

x < 5

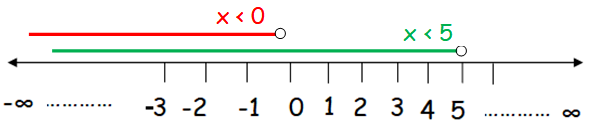
Sine we have "OR", the solution need not to be satisfied by both inequalities.

Hence the required interval notation for the given inequalities is (-∞, 5)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

HOW TO REPRESENT THE GIVEN INEQUALITIES IN INTERVAL NOTATION

AND

OR

Recent Articles

Digital SAT Math Problems and Solutions (Part - 62)

SAT Math Resources (Videos, Concepts, Worksheets and More)

Worksheet on Proving Trigonometric Identities