RELATION BETWEEN GCD AND LCM OF POLYNOMIALS PRACTICE QUESTIONS

Find the LCM of each pair of the following polynomials

1) x² - 5x + 6, x² + 4x - 12 whose GCD is (x - 2)

Solution

2) x⁴ + 3x³ + 6x² + 5x + 3, x⁴ + 2x² + x + 2 whose GCD is x² + x + 1

Solution

3) 2x³ + 15x² + 2x - 35, x⁴ + 8x² + 4x - 21 whose GCD is x + 7

Solution

4) 2x³ - 3x² - 9x + 5, 2x⁴ - x³ - 10x² - 11x + 8 whose GCD is 2x - 1

Solution

Find the other polynomial q(x) of each of the following, given that LCM and GCD and one polynomial p(x) respectively.

5)  (x + 1)² (x + 2)², (x + 1) (x + 2), (x + 1)² (x + 2)

Solution

6) (4x + 5)³ (3x - 7)³, (4x + 5) (3x - 7)², (4x + 5)³ (3x -7 )²

Solution

7) (x⁴ - y⁴)(x⁴ + x²y² + y⁴), x² - y², x⁴ - y⁴      Solution

8)  (x³ - 4x) (5x + 1), (5x² + x), (5x³ - 9x² - 2x)     Solution

9)  2(x + 1) (x² - 4), (x + 1), (x + 1) (x - 2)     Solution

10)  (x - 1) (x - 2) (x² -3x + 3), (x - 1), (x³ - 4x² + 6x - 3)

Solution

11)  2(x + 1) (x² - 4), (x + 1), (x + 1) (x - 2)        Solution

Detailed Solution

1) Solution :

LCM ⋅ GCD  =  f(x) ⋅ g(x)

LCM  =  [f(x) ⋅ g(x)]/GCD

f(x)  =  x² - 5x + 6

g(x)  =  x² + 4x - 12

GCD = (x - 2)

x² - 5x + 6 = (x - 2 )(x - 3)

x² + 4x - 12 = (x + 6)(x - 2)

LCM = (x - 2)(x - 3)(x + 6)(x - 2)/(x - 2)

By canceling common factors, we get

LCM  =  (x - 2) (x - 3) (x + 6)

So, the required LCM is (x - 2) (x - 3) (x + 6).

2) Solution :

x⁴ + 3x³ + 6x² + 5x + 3, x⁴ + 2x² + x + 2 whose GCD is x² + x +1 

LCM  =  [f(x) ⋅ g(x)]/GCD

f(x) = x⁴ + 3x³ + 6x² + 5x + 3

g(x) = x⁴ + 2x² + x + 2

GCD = x² + x + 1

LCM  = [(x⁴ + 3x³ + 6x² + 5x + 3) (x⁴ + 2x² + x + 2) ]/(x² + x + 1)

To simplify this, we have to use long division.

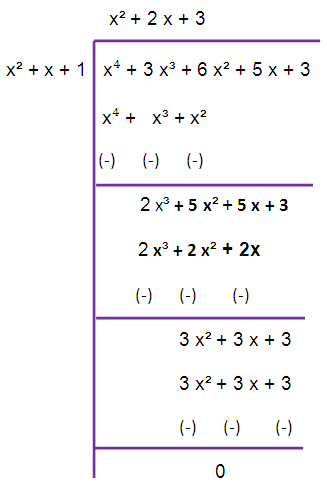
LCM  =  (x² + 2x + 3) (x⁴ + 2x² + x + 2)

So, the required LCM is (x² + 2x + 3) (x⁴ + 2x² + x + 2).

3) Solution :

2x³ + 15x² + 2x - 35, x⁴ + 8x² + 4x - 21 whose GCD is x + 7

LCM  =  [f(x) ⋅ g(x)]/GCD

f(x) = 2x³ + 15x² + 2x - 35

g(x) = x⁴ + 8x² + 4x - 21

GCD = x + 7

LCM  =  [(2x³ + 15x² + 2x - 35) (x⁴ + 8x² + 4x - 21)]/(x + 7)

To simplify this we have to use long division.

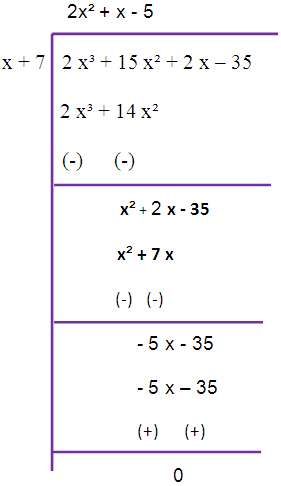
LCM  =  (2x² + x - 5) (x⁴ + 8x² + 4x - 21)

So, the required LCM is  (2x² + x - 5) (x⁴ + 8x² + 4x - 21).

4) Solution :

2x³ - 3x² - 9x + 5, 2x⁴ - x³ - 10x² - 11x + 8 whose GCD is 2x - 1

LCM = [f(x) ⋅ g(x)]/GCD

f(x) = 2x³ - 3x² - 9x + 5

g(x) = 2x⁴ - x³ - 10x² - 11x + 8

GCD  =  2x - 1

LCM  =  [(2x³ - 3x² - 9x + 5) (2x⁴ - x³ - 10x² - 11x + 8)]/(2x - 1)

To simplify this we have to use long division.

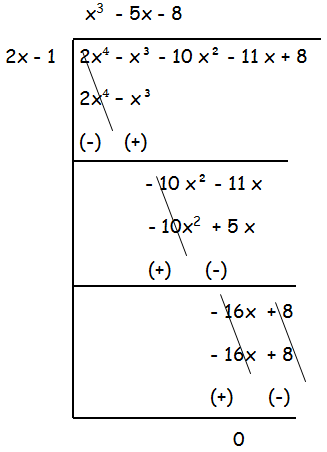
LCM  =  (x³ - 5x - 8) (2x³ - 3x² - 9x + 5)

So, the LCM is (x³ - 5x - 8) (2x³ - 3x² - 9x + 5).

5) Solution :

(x + 1)² (x + 2)², (x + 1) (x + 2), (x + 1)² (x + 2)

LCM ⋅ GCD  =  p(x) ⋅ q(x)

L.C.M = (x+1)² (x+2)²

GCD = (x+1) (x+2)

p(x) = (x+1)² (x+2)

q(x)  =  [LCM ⋅ GCD]/p(x)

q(x)  =  [(x+1)²(x+2)² (x+1) (x+2)]/(x+1)² (x+2)

q(x)  =  (x+2)² (x+1)

So, the other polynomial is (x+2)² (x+1).

6) Solution :

(4x+5)³ (3x-7)³, (4x+5) (3x-7)², (4x+5)³ (3x-7)²

LCM ⋅ GCD  =  p(x) ⋅ q(x)

LCM  =  (4x+5)³ (3x-7)³

GCD  =  (4x+5) (3x-7)²

p(x)  =  (4x+5)³ (3x-7)²

q(x)  =  [LCM ⋅ GCD]/p(x)

q(x)  =  [(4x+5)³ (3x-7)³(4x+5) (3x-7)²]/(4x+5)³ (3x-7)²

q(x)  =  (3x-7)³ (4x+5)

7) Solution :

(x⁴-y⁴)(x⁴+x²y²+y⁴), x²-y², x⁴-y⁴

LCM ⋅ GCD  =  p(x) ⋅ q(x)

LCM  =  (x⁴-y⁴)(x⁴+x²y²+y⁴)

GCD  =  x²-y²

p(x)  =  x⁴-y⁴

q(x)  =  [LCM ⋅ GCD]/p(x)

q(x)  =  [(x⁴-y⁴)(x⁴+x²y²+y⁴)(x²-y²)]/(x⁴-y⁴)

q(x)  =  (x⁴+x²y²+y⁴)(x²-y²)

So, the other polynomial is (x⁴+x²y²+y⁴)(x²-y²).

8) Solution :

(x³-4x) (5x+1), (5x²+x), (5x³-9x²-2x)

LCM ⋅ GCD  =  p(x) ⋅ q(x)

LCM  =  (x³-4x) (5x+1)

GCD  =  5x²+x  =  x(5x+1)

p(x)  =  5x³-9x²-2x ==>  x(5x²-9x-2)

x(5x²-9x-2)  ==> x (5x+1)(x-2)

q(x)  =  [LCM ⋅ GCD]/p(x)

q(x)  =  [(x³-4x) (5x+1)(5x+1)]/[x (5x+1)(x-2)]

q(x)  =  [(x²-4)(5x+1)]/(x-2)

q(x)  =  [(x+2)(x-2)(5x+1)]/(x-2)

q(x)  =  (x+2)(5x+1)

So, the other polynomial is (x+2)(5x+1).

9) Solution :

(x-1) (x-2) (x²-3x+3), (x-1), (x³-4x²+6x-3)

LCM ⋅ GCD  =  p(x) ⋅ q(x)

LCM  =  (x-1) (x-2) (x²-3x+3)

GCD  =  (x-1)

p(x)  =  x³-4x²+6x-3

q(x)  =  [LCM ⋅ GCD]/p(x)

         =  [(x-1)(x-2)(x²-3x+3)(x-1)]/(x³-4x²+6x-3)

let us use synthetic division to find factors of the cubic polynomial.

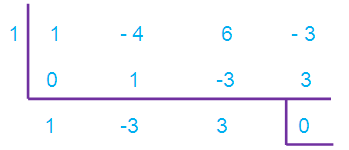
=  [(x-1)(x-2) (x²-3x+3)(x-1)]/(x-1) (x²-3x+3)

=  (x-2)(x-1)

So, the other polynomial is (x-2)(x-1).

10) Solution :

2(x+1) (x²-4), (x+1), (x+1) (x-2)

LCM ⋅ GCD  =  p(x) ⋅ q(x)

LCM  =  2(x+1) (x²-4)

GCD  =  (x+1)

p(x)  =  (x+1) (x-2)

q(x)  =  [LCM ⋅ GCD]/p(x)

q(x)  =  [2(x+1) (x²-4)(x+1)]/(x+1) (x-2)

q(x)  =  [2(x+1) (x+2) (x-2) (x+1)]/(x+1) (x-2)

q(x)  =  2(x+1) (x+2)

So, the other polynomial is 2(x+1) (x+2).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.