MIDSEGMENT THEOREM

In a triangle, the segment joining the midpoints of any two sides will be parallel to the third side and half of its length.

It has been illustrated in the diagram shown below.

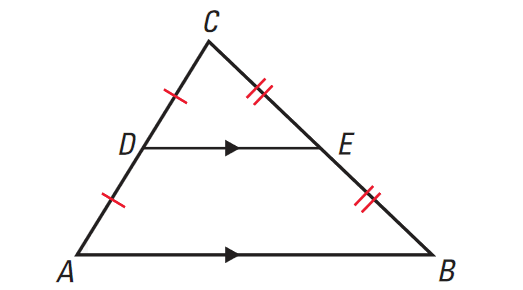
In the diagram shown above, we have

DE || AB and DE = 1/2 ⋅ AB

Midsegment

We may already know the four special types of segments of a triangle : perpendicular bisectors, angle bisectors, medians and altitudes. Another special type of segment is called a midsegment.

A midsegment of a triangle is a segment that connects the midpoints of two sides of a triangle.

Activity

You can form the three midsegments of a triangle by tracing the triangle on paper, cutting it out and folding.

Step 1 :

Fold one vertex onto another to find one midpoint.

Step 2 :

Repeat the process to find the other two midpoints.

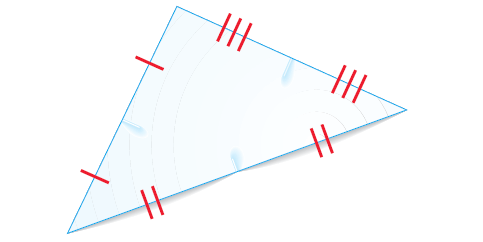
Step 3 :

Fold a segment that contains two of the mid points.

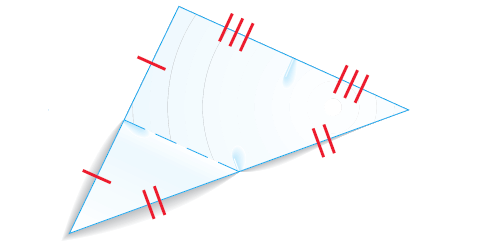
Step 4 :

Fold the remaining two midsegments of the triangle.

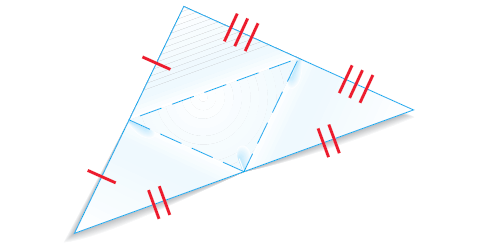
Solving Problems on Midsegment Theorem

Problem 1 :

In the diagram given below, show that the midsegment MN is parallel side JK and is half as long.

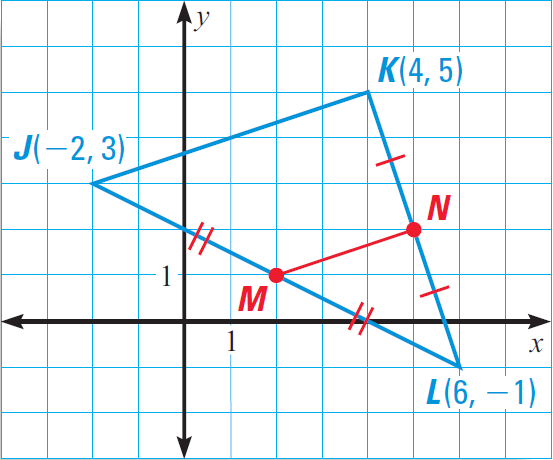
Solution :

Use the midpoint formula to find the coordinates of M and N.

Coordinates of M :

= ([-2 + 6]/2, [3 + (-1)]/2)

= (4/2, 2/2)

= (2, 1)

Coordinates of N :

= ([4 + 6]/2, [5 + (-1)]/2)

= (10/2 , 4/2)

= (5 , 2)

Now, find the slopes of JK and MN.

Slope of JK :

= [5 - 3]/[4 - (-2)]

= 2/6

= 1/3

Slope of MN :

Slope of MN = [2 - 1]/[5 - 2]

Slope of MN = 1/3

Because the slopes of JK and MN are equal, the sides JK and MN are parallel.

Using the distance formula, we have

MN = √10

JK = √40 = 2√10

So, MN is half as long as JK.

Problem 2 :

In the diagram given below, UW and VW are midsegments of triangle RST. Find UW and RT.

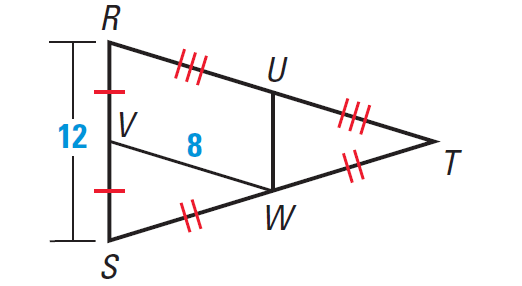
Solution :

By Midsegment Theorem, we have

UW = 1/2 ⋅ RS = 1/2 ⋅ 12 = 6

RT = 2 ⋅ VW = 2 ⋅ 8 = 16

Problem 3 :

Write a coordinate proof of the Midsegment Theorem.

Solution :

Place points A, B and C in convenient positions in a coordinate plane such that each coordinate is a multiple of 2.

(If each coordinate is a multiple of 2, it will be easier to divide by 2, when we find the mid point)

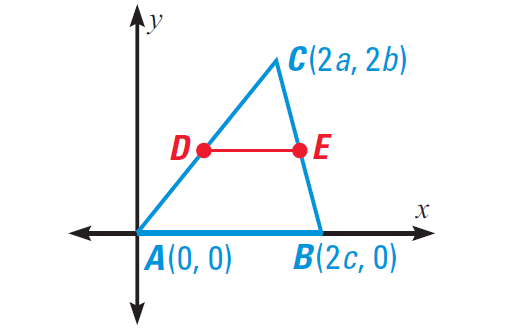
Coordinates of D :

= ([2a + 0]/2, [2b + 0]/2)

= (a , b)

Coordinates of E :

= ([2a + 2c]/2, [2b + 0]/2)

= (a + c, b)

Find the slope of midsegment DE :

= [b - b]/[a + c - a]

= 0/c

= 0

Find the slope of AB :

The side AB is on x-axis.

Because the slope of x-axis is zero, the slope of AB is also zero.

That is,

Slope of AB = 0

Because the slopes of DE and AB are equal, the sides DE and AB are parallel.

Find the lengths of DE and AB :

DE = |a + c - a| = |c| = c

AB = |2c - 0| = |2c| = 2c

The length of DE is half the length of AB.

Problem 4 :

The mid points of a triangle are P(4, 2), Q(2, 3) and R(5, 4). What are the coordinates of the vertices of the triangle.

Solution :

Plot the midpoints P(4, 2), Q(2, 3) and R(5, 4) in a coordinate plane.

Connect these midpoints to form the midsegments PQ, QR and PR.

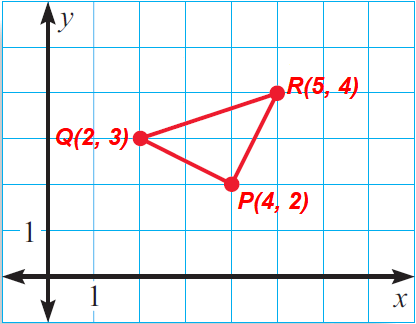
Find the slopes of the midsegments.

Slope of the midsegment PQ :

= (3 - 2)/(2 - 4)

= -1/2

Slope of the midsegment QR :

= (4 - 3)/(5 - 2)

= 1/3

Slope of the midsegment PR :

= (4 - 2)/(5 - 4)

= 2/1

= 2

Each midsegment contains two of the triangle's midpoints and is parallel to the side that contains the third midpoint.

Now, we know a point on each side of the triangle and the slope of each side.

Let us consider a line through the midpoint P and parallel to QR.

Because the line is parallel to QR, the slope of the line and slope of the midsegment QR are equal.

Then, the slope of the line is 1/3.

Using the slope 1/3, we can draw a line through the midpoint P and parallel to QR as shown below.

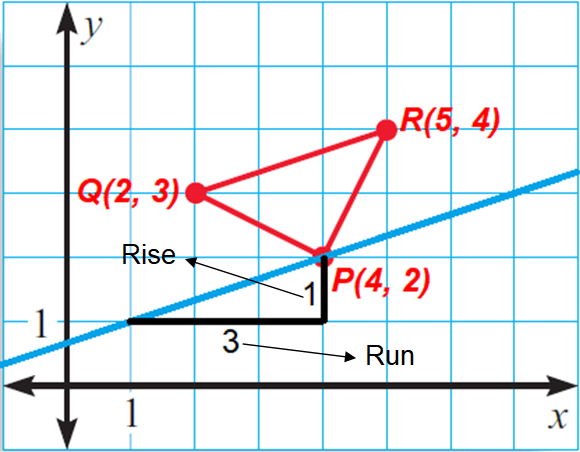
Similarly we can draw the other two lines through the midpoints Q, R and parallel to the midsegments PR and PQ respectively as shown below.

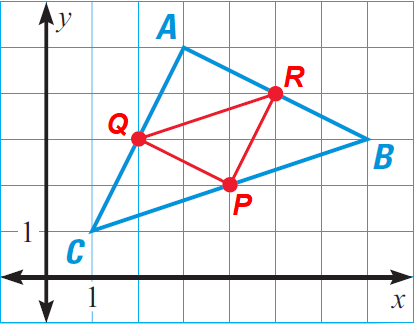
The lines intersect at A(3, 5), B(7, 3) and C(1, 1) which are the vertices of the triangle.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.