FIND OTHER POLYNOMIAL WHEN ONE POLYNOMAILS ITS LCM AND GCD ARE GIVEN

Find the other polynomial q(x) of each of the following, given that LCM and GCD and one polynomial p(x) respectively.

Example 1 :

(x + 1)² (x + 2)², (x + 1) (x + 2), (x + 1)² (x + 2)

Solution :

(x + 1)² (x + 2)², (x + 1) (x + 2), (x + 1)² (x + 2)

LCM ⋅ GCD  =  p(x) ⋅ q(x)

L.C.M = (x + 1)² (x + 2)²

GCD = (x + 1) (x + 2)

p(x) = (x+1)² (x+2)

q(x) = [LCM ⋅ GCD]/p(x)

q(x) = [(x + 1)²(x + 2)² (x + 1) (x + 2)]/(x + 1)² (x + 2)

q(x) = (x + 2)² (x + 1)

So, the other polynomial is (x + 2)² (x + 1).

Example 2 :

(4 x +5)³ (3x - 7)³, (4x + 5) (3x - 7)², (4x + 5)³ (3x - 7)²

Solution :

(4x + 5)³ (3x - 7)³, (4x + 5) (3x - 7)², (4x + 5)³ (3x - 7)²

LCM ⋅ GCD  =  p(x) ⋅ q(x)

LCM = (4x + 5)³ (3x - 7)³

GCD = (4x + 5) (3x - 7)²

p(x) = (4x + 5)³ (3x - 7)²

q(x) = [LCM ⋅ GCD]/p(x)

q(x)  =  [(4x + 5)³ (3x - 7)³(4x + 5) (3x - 7)²]/(4x + 5)³ (3x - 7)²

q(x) = (3x - 7)³ (4x + 5)

So, the other polynomial is (3x - 7)³ (4x + 5).

Example 3 :

(x⁴ - y⁴)(x⁴ + x²y² + y⁴), x² - y², x⁴ - y⁴

Solution :

(x⁴ - y⁴)(x⁴ + x²y² + y⁴), x² - y², x⁴ - y⁴

LCM ⋅ GCD = p(x) ⋅ q(x)

LCM = (x⁴ - y⁴)(x⁴ + x²y² + y⁴)

GCD = x² - y²

p(x) = x⁴ - y⁴

q(x) = [LCM ⋅ GCD]/p(x)

q(x) = [(x⁴ - y⁴)(x⁴ + x²y² + y⁴)(x² - y²)]/(x⁴ - y⁴)

q(x) = (x⁴ + x²y² + y⁴)(x² - y²)

So, the other polynomial is (x⁴ + x²y² + y⁴)(x² - y²).

Example 4 :

(x³ - 4x) (5x + 1), (5x² + x), (5x³ - 9x² - 2x)

Solution :

(x³ - 4x) (5x + 1), (5x² + x), (5x³ - 9x² - 2x)

LCM ⋅ GCD = p(x) ⋅ q(x)

LCM = (x³ - 4x) (5x + 1)

GCD = 5x² + x = x(5x + 1)

p(x) = 5x³ - 9x² - 2x ==>  x(5x² - 9x -2)

x(5x² - 9x - 2)  ==> x (5x + 1)(x - 2)

q(x) = [LCM ⋅ GCD]/p(x)

q(x) = [(x³ - 4 x) (5x + 1)(5x + 1)]/[x (5x + 1)(x - 2)]

q(x) = [(x² - 4 )(5x + 1)]/(x - 2)

q(x) = [(x + 2)(x - 2)(5x + 1)]/(x - 2)

q(x) = (x + 2)(5x + 1)

So, the other polynomial is (x + 2)(5x + 1).

Example 5 :

(x - 1) (x - 2) (x² - 3x + 3), (x - 1), (x³ - 4x² + 6x - 3)

Solution :

(x - 1) (x - 2) (x² - 3x + 3), (x - 1), (x³ - 4x² + 6x - 3)

LCM ⋅ GCD  =  p(x) ⋅ q(x)

LCM = (x - 1) (x - 2) (x² - 3x + 3)

GCD = (x-1)

p(x) = x³ - 4x² + 6x - 3

q(x)  =  [LCM ⋅ GCD]/p(x)

=  [(x - 1)(x - 2)(x² - 3x + 3)(x - 1)]/(x³ - 4x² + 6x - 3)

let us use synthetic division to find factors of the cubic polynomial.

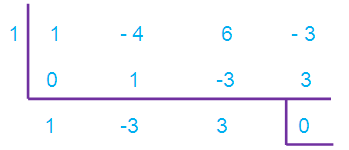
=  [(x - 1)(x - 2) (x² - 3x + 3)(x - 1)]/(x - 1) (x² - 3x + 3)

=  (x - 2)(x - 1)

So, the other polynomial is (x - 2)(x - 1).

Example 6 :

2(x + 1) (x² - 4), (x + 1), (x + 1) (x - 2)

Solution :

2(x + 1) (x² - 4), (x + 1), (x + 1) (x - 2)

LCM ⋅ GCD = p(x) ⋅ q(x)

LCM = 2(x + 1) (x² - 4)

GCD = (x + 1)

p(x) = (x + 1) (x - 2)

q(x)  =  [LCM ⋅ GCD]/p(x)

q(x) = [2(x + 1) (x² - 4)(x + 1)]/(x + 1) (x - 2)

q(x) = [2(x + 1) (x + 2) (x - 2) (x + 1)]/(x + 1) (x - 2)

q(x) = 2(x + 1) (x + 2)

So, the other polynomial is 2(x + 1) (x + 2).

Example 7 :

LCM = a³ - 10a² + 11a + 70, GCD = a - 7

p(x) = a² - 12a + 35

Solution :

(LCM ⋅ GCD = p(x) ⋅ q(x)

LCM = a³ - 10a² + 11a + 70

GCD = a - 7

p(x) = a² - 12a + 35

q(x)  =  [LCM ⋅ GCD]/p(x)

q(x) = [(a³ - 10a² + 11a + 70)  (a - 7)] / (a² - 12a + 35)

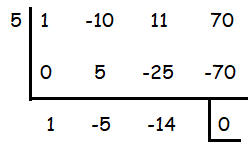
Factoring the cubic polynomial,  a³ - 10a² + 11a + 70

(a - 5) (a² - 5a - 14) are factors

a² - 5a - 14 = (a - 7)(a + 2)

Factoring the polynomial a² - 12a + 35, we get

= (a - 7)(a - 5)

q(x) = [ (a - 5) (a - 7)(a + 2)  (a - 7)] / (a - 7)(a - 5)

q(x) = (a + 2)(a - 7)

q(x) = a² + 2a - 7a - 14

= a² - 5a - 14

So, the required polynomial q(x) is a² - 5a - 14.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.