REFLECTION OVER X AXIS AND Y AXIS

When P(x, y) is reflected in the mirror line to become p'(x', y'), the mirror line perpendicularly bisects pp'

Thus, for every point of an object, the mirror line is perpendicularly bisects the line segment joining the point with its image. 

Reflection on x axis
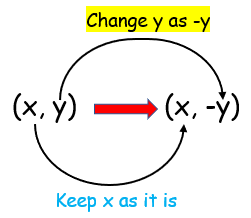Reflection on y axis
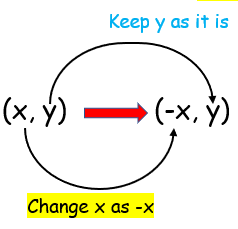Reflection about y = x
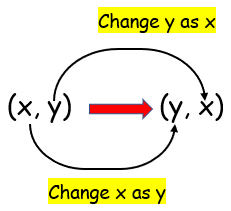Reflection about y = -x

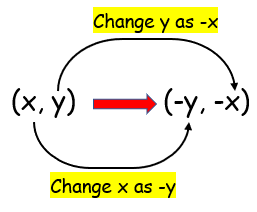Example 1 :

Find the image equation of

2x-y+3  =  0

reflected in the x-axis.

Solution :

Required transformation :

Reflection about x - axis, So replace y by -y.

Put y = -y and 

Original equation  ==>   2x-y+3  =  0

After reflection ==>  2x-(-y)+3  =  0

2x+y+3  =  0

So, image equation of the given equation is 2x+y+3  =  0.

Example 2 :

Find the image equation of

2x-3y  =  8

reflected in the y-axis.

Solution :

Required transformation :

Reflection about y - axis, So replace x by -x.

Put x = -x and 

Original equation  ==>   2x-3y  =  8 

After reflection ==>  -2x-3y  =  8

2x+3y  =  -8

So, image equation of the given equation is 2x+3y  =  -8

Example 3 :

Find the image equation of

y  =  2x²

under y  =  x

Solution :

Required transformation :

Reflection under y  =  x, so change x as y and y as x.

Put x = -y and y = x

Original equation  ==>   y  =  2x²

After reflection ==>  x  =  2y²

So, image equation of the given equation is x  =  2y².

Example 4 :

Find the image equation of

2x+3y  =  4

under y  =  x

Solution :

Required transformation :

Reflection under y  =  -x, so change x as -y and y as -x.

Put x = -y and y = -x

Original equation  ==>   2x+3y  =  4

After reflection ==>  2(-y)+3(-x)  =  4

-2y-3x  =  4

3x+2y+4  =  0

So, image equation of the given equation is 3x+2y+4  =  0.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.