PROPORTIONAL RELATIONSHIPS

Example 1 :

Examine the given table and determine if the relationship is proportional. If yes, determine the constant of proportionality.

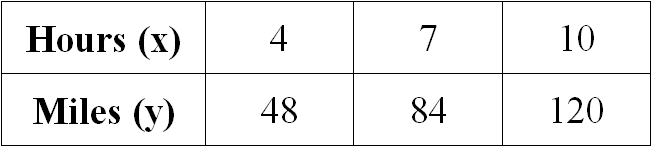
Solution :

Let us get the ratio of x and y for all the given values.

4/48 = 1/12

7/84 = 1/12

10/120 = 1/12

When we take ratio of x and y for all the given values, we get equal value for all the ratios.

Therefore the relationship given in the table is proportional.

When we look at the above table when x gets increased, y also gets increased, so it is direct proportion.

Then, we have

y = kx

Substitute x = 4 and y = 48.

48 = k(4)

12 = k

So, the constant of proportionality is 12.

Example 2 :

Examine the given table and determine if the relationship is proportional. If yes, determine the constant of proportionality.

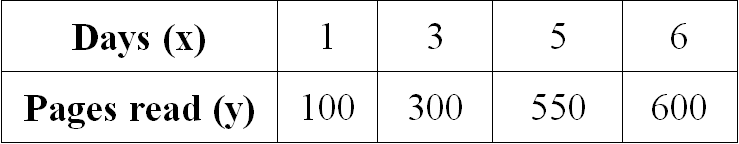
Solution :

Let us get the ratio of x and y for all the given values.

1/100 = 1/100

3/300 = 1/100

5/550 = 1/110

6/600 = 1/100

When we take ratio of x and y for all the given values, we don't get equal value for all the ratios.

Therefore the relationship given in the table is not proportional.

Example 3 :

Examine the given table and determine if the relationship is proportional. If yes, determine the constant of proportionality.

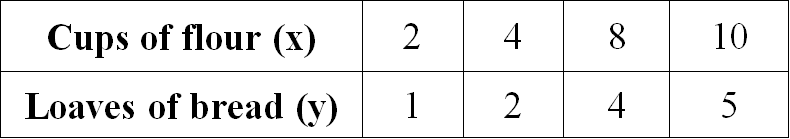
Solution :

Let us get the ratio of x and y for all the given values.

2/1 = 2

4/2 = 2

8/4 = 2

10/5 = 2

When we take ratio of x and y for all the given values, we get equal value for all the ratios.

Therefore the relationship given in the table is proportional.

When we look at the above table when x gets increased, y also gets increased, so it is direct proportion.

Then, we have

y = kx

Substitute x = 2 and y = 1.

1 = k(2)

1/2 = k

So, the constant of proportionality is 1/2.

Question 4 :

Examine the given table and determine if the relationship is proportional. If yes, determine the constant of proportionality.

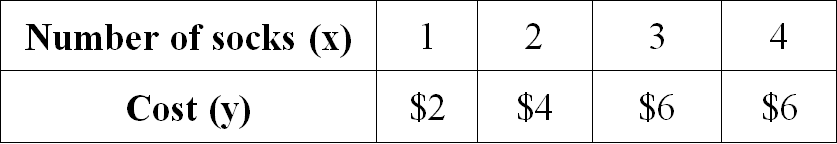
Solution :

Let us get the ratio of x and y for all the given values.

1/2 = 1/2

2/4 = 1/2

3/6 = 1/2

4/6 = 2/3

When we take ratio of x and y for all the given values, we don't get equal value for all the ratios.

Therefore the relationship given in the table is not proportional.

Example 5 :

Examine the given table and determine if the relationship is proportional. If yes, determine the constant of proportionality.

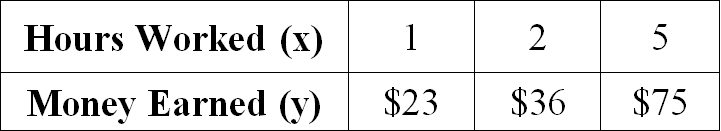
Solution :

Let us get the ratio of x and y for all the given values.

1/23 = 1/23

2/36 = 1/18

5/75 = 1/15

When we take ratio of x and y for all the given values, we don't get equal value for all the ratios.

Therefore the relationship given in the table is not proportional.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.