PROBLEMS ON AREA AND PERIMETER OF COMBINED FIGURES

Example 1 :

Find the perimeter and area of the following figures:

Solution :

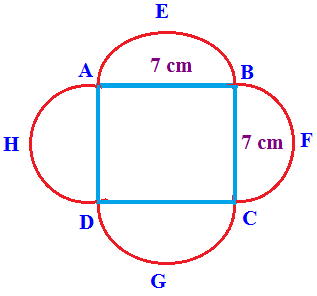
In the above figure we have four semi circles and one square. To find the perimeter, we have to add the sum of four semicircles and a square.

Radius  =  7/2  =>  3.5 cm   

Length of each side of square = 7 cm

The perimeter of the given figure

=  4 (perimeter of semicircles) + Perimeter of square

Perimeter of semi circle AEB  =  Π r

=  (22/7) x 3.5

=  22 x 0.5

=  11

Perimeter of 4 semi circles  =  4 (11)

=  44 cm

Perimeter of square = 4a

=  28 cm

The perimeter of the given figure = 44 cm + 28 cm

= 72 cm

Area of 1 semi circle = Π r²/2

=  (1/2) x (22/7) x (7/2)²

=  (1/2) x (22/7) x (7/2) x (7/2)

=  (1/2) x 11 x (7/2)

=  77/4

=  19.25 cm²

Area of 4 semi circles  =  4 (19.25)

=  77

Area of square  =  a²

=  7x7

=  49 cm²

Area of given figure

= Area of 4 semi circles + Area of square

=  77 + 49 

=  126 cm²

Example 2 :

Find the area of shaded portion.

Solution :

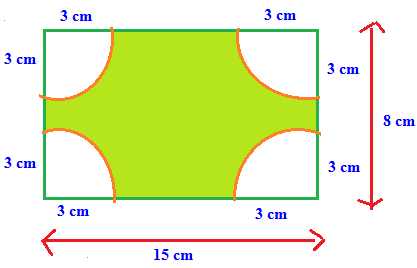
Area of shaded portion

=  Area of rectangle - Area of 4 quadrants of circle

Area of rectangle  =  Length x Width

Length of rectangle  =  15 cm

Width of rectangle  =  8 cm

=  15 x 8

=  120 cm²

Area of quadrant  =  Π r²/4

radius of quadrant = 3 cm

=  [(22/7) x 3²]/4       

=  (22 x 3 x 3)/(7 x 4)   

=  198/28

Area of 4 quadrant = 4 x 198/28

=  198/7

=  28.28 cm²

Area of shaded portion  =  120 - 28.28

=  91.715 cm²

Example 3 :

The kitchen in Mario’s Italian restaurant is 18  meters long and 12 meters wide. A square  pantry is connected to the kitchen area. The  pantry is 3 meters wide. What is the total area  of the kitchen and pantry?

Solution :

Total area of the kitchen and pantry  =  Area of rectangle + Area of square

Area of rectangle  =  length x width

Area of square  =  a x a

Length of rectangle  =  18 m and width  =  12 m

Side length square pantry  =  3 m

Required area  =  (18 x 12) + (3 x 3)

=  216+9

=  225 square meter

Example 4 :

The area of  triangle QTU is 6 square units, and the  area of triangle RSU is 6 square units. The  dimensions in the figure below are labeled in  units. What is the area of  triangle STU in square  units?

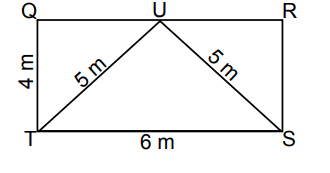
Solution :

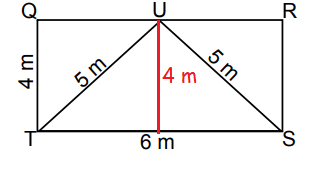
Area of triangle SUT 

=  Area of rectangle TQRS - 2(Area of TQU)

Area of rectangle  =  length x width

=  6 x 4

=  24 m²

TU²  =  TQ² + UQ²

5²  =  4² + UQ²

UQ²  =  25-16

UQ²  =  9

UQ  =  3

Area of triangle TQU  =  (1/2) x base x height

=  (1/2) x 3 x 4

=  6

Area of triangles TQU and SRU  =  12

Required area  =  24 - 12

=  12 m²

Example 5 :

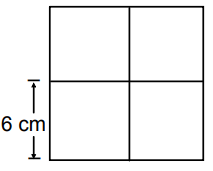
The figure below is divided into four small  squares. The sides of each small square are 6  cm long. What is the area, in square  centimeters, of the entire figure?

Solution :

Area of square  =  a x a

Side length  =  6 + 6  ==>  12 cm

Area of square  =  12 x 12

=  144 cm²

Example 6 :

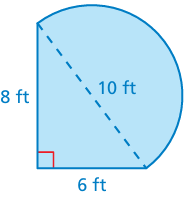
The figure is made up of a semicircle and a triangle. Find the perimeter

Solution :

Area of composite figure = area of triangle + area of semicircle

= (1/2) x base x height + (1/2) πr²

Base of triangle = 6 ft, height of triangle = 8 ft

radius of semicircle = 5 ft

= (1/2) x 6 x 8 + (1/2) π(5)²

= 24 + 0.5 x 3.14 x 25

= 24 + 39.25

= 63.25 square feet.

Example 7 :

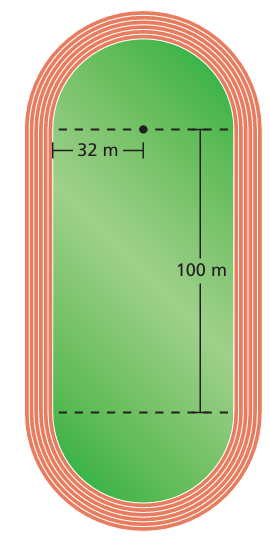
The running track is made up of a rectangle and two semicircles. Find the perimeter.

Solution :

Radius of semicircle = 32 m

length of rectangle = 100 m

= 2 πr + 2(length of rectangle)

= 2 x 3.14 x 32 + 2(100)

= 200.96 + 200

= 400.96 square meter

Example 8 :

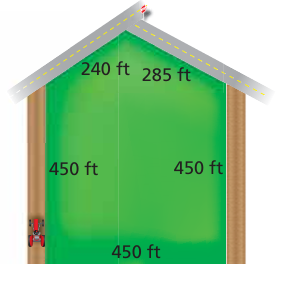
A section of land is to be fenced in for a horse pasture.

a. Find the perimeter of the pasture.

b. Fencing costs $27 per yard. How much will it cost to fence in the pasture?

Solution :

a)  Perimeter of the pasture

= 450 + 450 + 450 + 240 + 285

= 3(450) + 240 + 285

= 1350 + 240 + 285

= 1875 ft

b) Fencing cost = $27 per yard

1 yard = 3 ft

1 ft = 1/3 yard

1875 ft = 1875/3 yards

= 625 yards

Required cost = 625 x 27

= $16875

Example 9 :

The inner circumference is 352 mm and outer is 396 mm. Find the width of circular design.

Solution :

Let r be the radius of smaller circle and R be the radius of larger circle.

Circumference of smaller circle = 2πr

Circumference of smaller circle = 2πR

Width = R - r

= 63.05 - 56.05

Width = 7 mm

So, width of the circular design is 7 mm.

Example 10 :

A rectangular field is 48 m long and 12 m wide. How many right triangular flower beds can be laid in this field, if sides including the right angle measure 2 m and 4 m, respectively?

Solution :

Area of rectangle = 48 x 12

= 576 square meter

Area of right triangle = (1/2) x 2 x 4

=4 square meter

Number of flower beds = 576/4

= 144 flower beds

Example 11 :

A design is made up of four congruent right triangles as shown in figure. Find the area of the shaded portion.

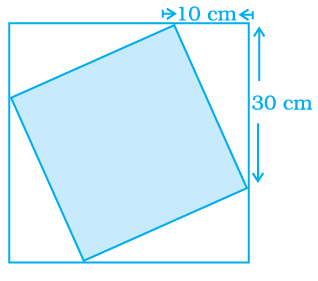
Solution :

At corners we have right triangle. 

Length of hypotenuse = side length of square

l = √10² + 30²

= √(100 + 900)

= √1000

= 10 √10

Area of square = (side)²

= (10 √10)²

= 100(10)

= 1000 square cm

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.