Practice Questions on Factorization

PRACTICE QUESTIONS ON FACTORIZATION

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

Part A

Factories the following monomials

(1) 25n²

(2) 18xy

(3) 12y

(4) 21y²

(5) 81a

(6) 92q

(7) 36x³

(8) 24h

(9) 48x²

(10) x²y³

Solution

Answers :

(1) 5 ⋅ 5 ⋅ n ⋅ n

(2) 2 ⋅ 3 ⋅ 3 ⋅ x ⋅ y

(3) 2 ⋅ 2 ⋅ 3 ⋅ y

(4) 3 ⋅ 7 ⋅ y ⋅ y

(5) 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ a

(6) 2 ⋅ 2 ⋅ 23 ⋅ q

(7) 2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ x ⋅ x ⋅ x

(8) 2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ h

(9) 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ x ⋅ x

(10) x ⋅ x ⋅ y ⋅ y ⋅ y

Part B

Factor the following polynomials by grouping

(1) x² + xt + ax + at

(2) 2y³ + 4y² + y + 2

(3) xy - 5y - 2x + 10

(4) 6ax + 3bd - 2ad - 9bx

(5) 3x³ + 3x² - 6x - 6

(6) 2ax² - cx² + 6a - 3c

(7) 4a² + 5ab - 10b - 8a

(8) a²x + 3a²y - 9x - 27y

Solution

Answers :

(1) (x + t)(x + a)

(2) (y + 2)(2y² + 1)

(3) (x - 5)(y - 2)

(4) (2a - 3b)(3x - d)

(5) 3(x² - 2)(x + 1)

(6) (2a - c)(x² + 3)

(7) (4a + 5b)(a - 2)

(8) (x + 3y)(a + 3)(a - 3)

Part C

Factor the following polynomials using algebraic identities

(1) x² + 6xy + 9y²

(2) 4a² - 20ab + 25b²

(3) 2x² + 12xy + 18y²

(4) 2ab² - 16ab + 32a

(5) x² - 25y²

(6) 9m² - 16n²

(7) x⁴ - y⁴

(8) 8p⁴ - 18q⁴

Solution

Answers :

(1) (x + 3y)(x + 3y)

(2) (2a - 5b)(2a - 5b)

(3) 2(x + 3y)(x + 3y)

(4) 2a(b - 4)²

(5) (x + 5y)(x - 5y)

(6) (3m + 4n)(3m - 4n)

(7) (x²+ y²)(x + y)(x - y)

(8) 2(4p²+ 9q²)(2p + 3q)(2p - 3q)

Part D

Factoring linear expression

(1) 4x + 8

(2) 16a + 64b - 4c

(3) 36x - 16

(4) 35 + 21a

(5) 4a - 8b + 5ax - 10bx

Answers :

(1) 4(x + 2)

(2) 4(4a + 16b - c)

(3) 4(9x - 4)

(4) 7(5 + 3a)

(5) (a - 2b) (4 + 5x)

Part E

Factoring quadratic polynomial

(1) x² + 6x + 5

(2) x² + 2x - 35

(3) x² - 6x - 7

(4) x² - 18x + 65

(5) 3x² – 5x – 12

(6) 2x² + x - 6

Solution

Answers :

(1) (x + 1)(x + 5)

(2) (x - 5)(x + 7)

(3) (x - 7)(x + 1)

(4) (x - 5)(x - 13)

(5) (3x + 4)(x - 3)

(6) (x + 2)(2x - 3)

Part F

Factor sum of difference of the cubes :

(1) m³ + 8

(2) a³ - 125

(3) x³ + 8y³

(4) 8x³ - 125y³

(5) 27x³ + 64y³

(6) 2m³ - 54n³

Solution

Answers :

(1) (m + 2)(m² - 2m + 4)

(2) (a - 5)(a² + 5a + 25)

(3) (x + 2y)(x² - 2xy + 4y²)

(4) (2x - 5y)(4x² + 10xy + 25y²)

(5) (3x + 4y)(9x² - 12xy + 16y²)

(6) 2(m - 3n)(m² + 3mn + 9n²)

Part G

Factor the following cubic polynomial

(1) x³ - 2x² - 5 x + 6

(2) 4x³ - 7x + 3

(3) x³-23x²+142x-120

(4) 4x³-5x²+7x-6

(5) x³ - 7x + 6

(6) x³ +13x²+32x+20

Solution

(1) (x - 1) (x - 3) (x + 2)

(2) (x - 1)(2x - 1)(2x + 3)

(3) (x - 1)(x - 10)(x - 12)

(4) (x - 1)(4x²- x + 6).

(5) (x - 1)(x + 3)(x - 2)

(6) (x + 1)(x + 10)(x + 2)

Question 1 :

Solve the following quadratic equations by factorization method :

√2x² + 7x + 5√2 = 0

Solution

Question 2 :

Solve the following quadratic equations by factorization method :

10x² - x - (1/5) = 0

Solution

Question 3 :

The number of volleyball games that must be scheduled in a league with n teams is given by G (n) = (n² - n)/2 where each team plays with every other team exactly once. A league schedules 15 games. How many teams are in the league?

Solution

Question 4 :

Victor is y years old. His brother Fred is four years old than Victor. The product of their ages is 780.

(a) Set up an equation to represent this information.

(b) Solve your equation from (a) to find Victor’s age.

Solution

Question 5 :

A rectangular field is 30m longer than wide. The area of the field is 8800 m² Work out the perimeter of the field.

Solution

Question 6 :

Shown is a right angled triangle. Show that

11x² − 62x − 105 = 0

and solve for x.

Solution

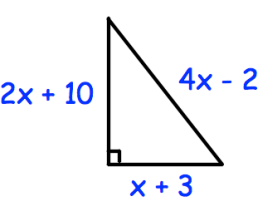
Question 7 :

Shown is a right angled triangle with sides are measured in centimeters.

(a) Show that x² − 5x − 14 = 0

(b) Solve for x.

Solution

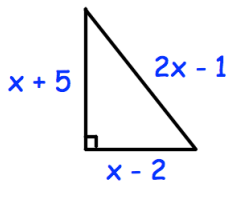
Question 8 :

The surface area of the cuboid is 270 cm².

(a) Show x² + 4x − 45 = 0

(b) Solve for x

Solution

Answer Key

x = -5√2/2 and x = -√2

2) x = 1/5 (or) x = -1/10

3) Hence 6 teams are in the league.

Age of Victor = 26 years

Age of Fred = 26 + 4 ==> 30 years.

5) width of the rectangle is 80 m and width is 110 m

6) the value of x is 35/9.

7) x = -2 and x = 7

8) the value of x is 5 cm.

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

About Us | Contact Us | Privacy Policy

PRACTICE QUESTIONS ON FACTORIZATION

Answer Key

Recent Articles

Quantitative Reasoning Questions and Answers

Coin Tossing Probability

10 Hard SAT Math Questions (Part - 39)