POLYGON INSCRIBED IN A CIRCLE

If all of the vertices of a polygon lie on a circle, the polygon is inscribed in the circle and the circle is circumscribed about the polygon.  The polygon is an inscribed polygon and the circle is a circumscribed circle.  

Theorems About Inscribed Polygons

Theorem 1 :

If a right triangle is inscribed in a circle, then the hypotenuse is a diameter of the circle.  Conversely, if one side of an inscribed triangle is a diameter of the circle, then the triangle is a right triangle and the angle opposite the diameter is the right angle.

It is illustrated in the diagram shown below. 

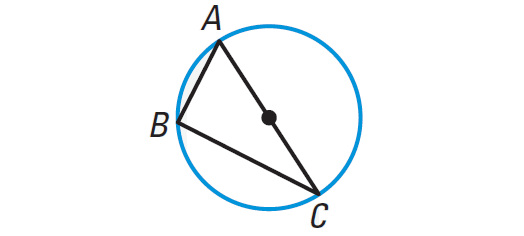
In the diagram shown above, ∠B  is a  right angle if and only if AC is  a diameter of the circle.

Theorem 2 :

A quadrilateral can be inscribed in a  circle if and only if its opposite angles are supplementary.

It is illustrated in the diagram shown below. 

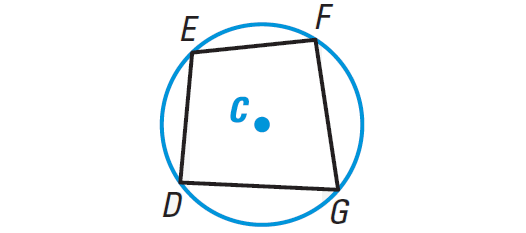
In the diagram shown above, D, E, F, and G lie on some circle with center at C, if and only if

m∠D + m∠F  =  180°  and  m∠E + m∠G  =  180°

Using Theorems 1 and 2

Example 1 :

Find the value of x in the diagram shown below. 

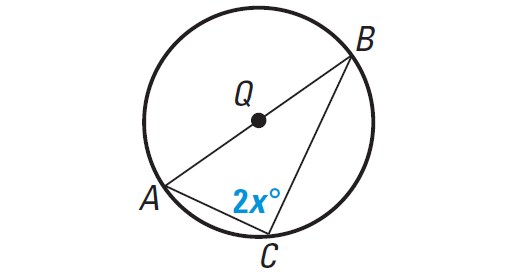
Solution :

AB is diameter.  So, ∠C  is a right angle and  m∠C = 90°.

2x°  =  90°

2x  =  90

Divide each side by 2. 

2x/2  =  90/2

x  =  45

Example 2 :

Find the value of y and z in the diagram shown below. 

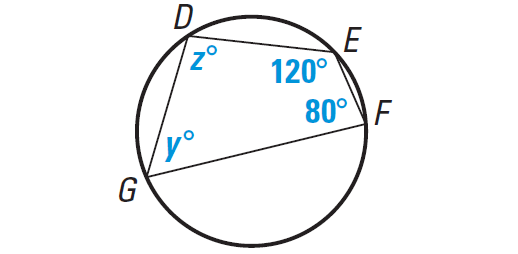
Solution :

DEFG is inscribed in a circle, so opposite angles are supplementary.

Using an Inscribed Quadrilateral

Example 3 :

In the diagram, polygon ABCD is inscribed in the circle with center P.  Find the measure of each angle.

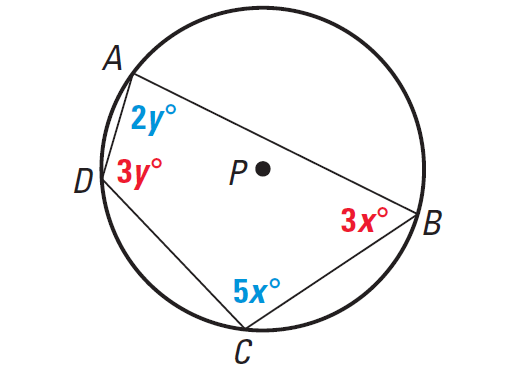
Solution :

ABCD is inscribed in a circle, so opposite angles are supplementary.

So, we have 

3x + 3y  =  180 -----(1) 

5x + 2y  = 180 -----(2)

To solve the above system of linear equations, we can solve the first equation for y.

(1)-----> 3x + 3y  =  180

3(x + y)  =  180

Divide each side by 3. 

3(x + y) / 3  =  180 / 3

x + y  =  60

Subtract x from each side. 

y  =  60 - x -----(3)

Plug y  =  60 - x in the second equation. 

(2)-----> 5x + 2(60 - x)  =  180

5x + 120 - 2x  =  180

Simplify.  

3x + 120  =  180

Subtract 120 from each side. 

3x  =  60

Divide each side by 3. 

3x / 3  =  60 / 3

x  =  20

Plug x  =  20 in the third equation. 

(3)-----> y  =  60 - 20

y  =  40

We get x  =  20 and y  =  40. 

So, we have 

m∠A  =  2y°  =  2(40°)  =  80°

m∠B  =  3x°  =  3(20°)  =  60°

m∠C  =  5x°  =  5(20°)  =  100°

m∠D  =  3y°  =  3(40°)  =  120°

Example 4 :

In Figure, ∠ABC = 69°, ∠ACB = 31°, find ∠BDC.

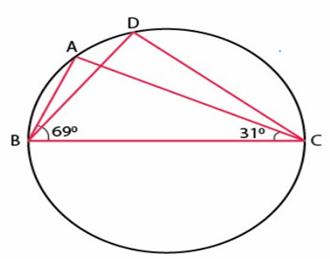
Solution :

In triangle ABC,

∠ABC = 69°, ∠BCA = 31° and ∠BAC = ?

∠ABC + ∠BCA + ∠BAC = 180

69 + 31 + ∠BAC = 180

∠BAC = 180 - (69 + 31)

= 180 - 100

= 80

Angle measures created by the same arc will be equal.

∠BAC = ∠BDC = 80

Example 5 :

In Figure, ∠PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠OPR.

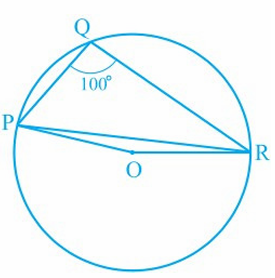
Solution :

Sum of opposite angles is 180 degree.

∠PQR + ∠PSR = 180

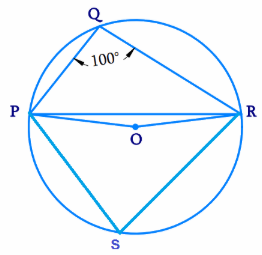
100 + ∠PSR = 180

∠PSR = 180 - 100

∠PSR = 80

∠POR = 2∠PSR

∠POR = 2(80)

= 160

∠POR + ∠OPR + ∠ORP = 180

Here ∠OPR = ∠ORP because equal sides will create equal angles.

160 + ∠OPR + ∠OPR = 180

2∠OPR = 180 - 160

2∠OPR = 20

∠OPR = 20/2

∠OPR = 10

Example 6 :

In figure, if OA = 5 cm, AB = 8 cm and OD is perpendicular to AB, What is the length of CD ?

a) 2 cm     (b) 3 cm      (c) 4 cm    (d) 5 cm

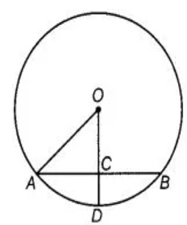
Solution :

OA = 5 cm, AB = 8 cm

AC = AB/2 ==> 8/2

AC = 4 cm

In triangle OAC,

OA² = OC² + AC²

5² = OC² + 4²

25 = OC² + 16

OC² = 25 - 16

OC² = 9

OC = 3 cm

OC and CD will be equal, because these two are radii.

OD = 5 cm

OC + CD = 5

3 + CD = 5

CD = 5 - 3

CD = 2 cm

Example 7 :

In figure, if ∠OAB = 40°, then what is the measure of ∠ACB?

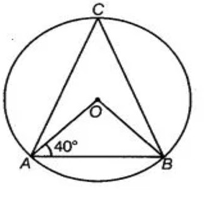
Solution :

In triangle OAB, 

∠OAB + ∠OBA + ∠AOB = 180

40 + 40 + ∠OAB = 180

∠OAB = 180 - 80

∠OAB = 100

∠ACB = ∠OAB/2

∠ACB = 50

Example 8 :

Use the Inscribed Right Triangle-Diameter Theorem to set up and solve an equation to find the value of x.

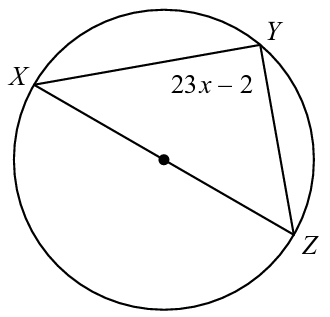
Solution :

Since XZ is the diameter of the circle,

∠XYZ = 90

23x - 2 = 90

23x = 90 + 2

23x = 92

x = 92/23

x = 4

So, the value of x is 4.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.