PATTERNS AND INDUCTIVE REASONING

Example 1 :

Sketch the next figure in the pattern.

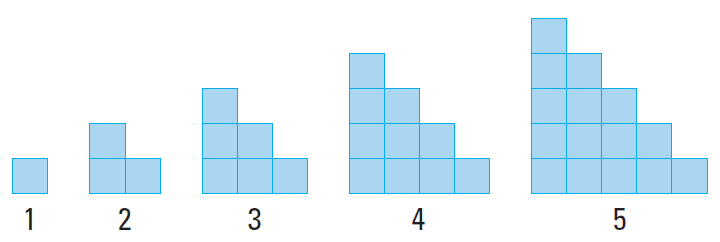
Solution :

Each figure in the pattern looks like the previous figure with another row of squares added to the bottom. Each figure looks like a stairway.

So, the sixth figure in the pattern must have six squares in the bottom row.

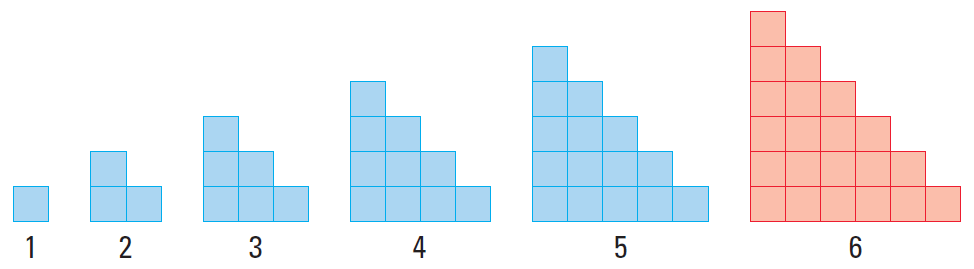
Example 2 :

Describe a pattern in the sequence of numbers. Predict the next number.

1, 4, 16, 64, ......

Solution :

Each number is four times the previous number. 

So, the next number is 256.

Example 3 :

Describe a pattern in the sequence of numbers. Predict the next number. 

-5,-2, 4, 13, ......

Solution : 

When we look at the above sequence of numbers, the following pattern comes into picture. 

When we add 3 to the first number "-5", we get the second number "-2". To get the third number, we have to add 6 to the second number "-2". To get the fourth number, we have to add 9 to the third number "13".

So, the above sequence of numbers is being generated by adding the consecutive multiples of 3. To get the fifth number, we have to add the next multiple of three, which is 12 to the fourth number. 

Then, the number is 13 + 12  =  25.

Example 4 :

Look carefully at the following figures. Then use inductive reasoning to make a conjecture about the next figure in the pattern.  

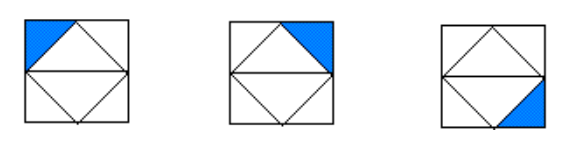
Solution :

If we have carefully observed the above pattern, we can have the following points.

(i) In the first figure, the shaded portion is at the top left corner.

(ii) In the second figure, the shaded portion is at the top right corner.

(iii) In the third figure, the shaded portion is at the bottom right corner.

Thus, in the fourth figure, we must have the shaded portion at the bottom left corner as given below.

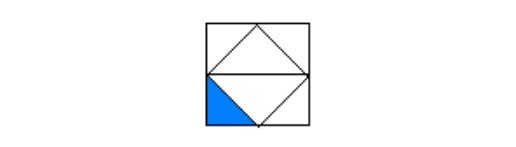
Example 5 :

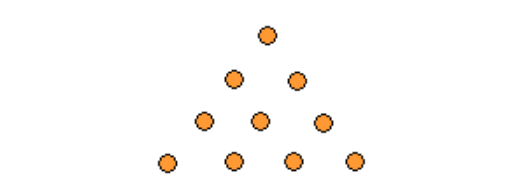
Look at the pattern below. Can we draw the next figure or next set of dots using inductive reasoning?

Solution :

The trick is to see that one dot is always placed between and above two dots.

At the very bottom row, we have one dot in the first figure, two dots in the second figure and three dots in the third figure.

Thus, the next figure must have four dots at the very bottom row.

Keeping this in mind, our next figure must look like this :

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.