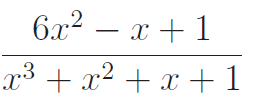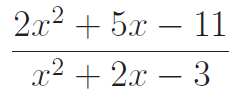PARTIAL FRACTION WORKSHEET FOR GRADE 11
A rational expression f(x)/g(x) is called a proper fraction if the degree of f(x) is less than degree of g(x), where g(x) can be factored into linear factors and quadratic factors without real zeros. Now f(x) g(x) can be expressed in simpler terms, namely, as a sum of expressions of the form
How to resolve the given linear fraction as partial fraction ?
First we have to factorize the denominator into prime factors. There are three types in partial fraction.
Linear Factors, No Factor is Repeated
When the factors of the denominator of the given fraction are all linear factors none of which is repeated. We write the partial fraction as follows.
(x +3)/(x + 1) (x - 2)
here the denominator is in the form linear factors and no factor is repeated. So we can write the partial-fraction as
(x +3) / (x + 1) (x - 2) = [A/(x + 1)] + [B/(x - 2)]
where A and B are constants.
Linear Factors, Some of the Factors are Repeated
When the factors of the denominator of the given fraction are all linear factors none of which is repeated. We write the partial fraction as follows.
If a linear factor (a x + b) occurs n times as a factor of the denominator of the given fraction, then we can write the partial-fraction as
(x + 3)/(x - 2)³
= [A/(x - 2)] + [B/(x - 2)²] + [C/(x - 2)³]
where A, B and C are constants.
Quadratic Equation in the Denominator
If a quadratic equation a x² + b x + c which is not favorable into linear factors occurs only once as factor of the denominator of the given fraction, then we can write the partial fraction as
Practice Problems
Resolve the following rational expressions into partial fractions.
(1) 1/(x2-a2) Solution
(2) (3x + 1)/(x - 2) (x + 1) Solution
(3) x/(x2 + 1)(x - 1)(x + 2) Solution
(4) x/(x-1)3 Solution
(5) 1/(x4 - 1) Solution
(6) (x - 1)2 / (x3 + x) Solution
(7) (x2 + x + 1)/(x2 - 5x + 6) Solution
(8) (x3 + 2x + 1)/(x2 + 5x + 6) Solution
(9) (x + 12) / (x + 1)2 (x - 2) Solution
(12) (7 + x) / (1 + x)(1 + x2) Solution
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
SAT Math Resources (Videos, Concepts, Worksheets and More)
Nov 21, 24 06:23 AM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Digital SAT Math Problems and Solutions (Part - 75)
Nov 21, 24 06:13 AM
Digital SAT Math Problems and Solutions (Part - 75) -
Digital SAT Math Problems and Solutions (Part - 74)
Nov 20, 24 08:12 AM
Digital SAT Math Problems and Solutions (Part - 74)
