OPERATIONS WITH MATRICES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Equality of Matrices :
Two matrices A = [aij]mxn and B = [bij]mxn are said to be equal if
(i) They are of same order and
(ii) Each element of A is equal to the corresponding element of B, that is aij = bij for all i and j.
For example, the matrices

are not equal as the orders of the matrices are different.
Multiplication of a matrix by a scalar :
For a given matrix A = [aij]mxn and a scalar (real number) k, we define a new matrix B = [bij]mxn, where
bij = kaij
for all i and j.
Thus, the matrix B is obtained by multiplying each entry of A by the scalar k and written as B = kA. This multiplication is called scalar multiplication.
(iii) Addition of matrices :
If A = [aij]mxn and B = [bij]mxn are two matrices of the same order, then the addition of A and B is a matrix C = [cij]mxn, where
cij = aij + bij
for all i and j.
The addition of two matrices A and B is denoted by A+B. Addition is not defined for matrices of different orders.
(iv) Negative of a matrix :
The negative of a matrix A = [aij]mxn is denoted by -A and is defined as -A = (- 1)A.
That is,
-A = [bij]mxn, where bij = aij
for all i and j.
(v) Subtraction of matrices :
If A = [aij]mxn B = [bij]mxn are two matrices of the same order, then subtraction A - B is defined as A - B = [cij]mxn, where
cij = aij - bij
for all i and j.
Operations with Matrices - Examples
Question 1 :
Find the values of x, y and z from the matrix equation
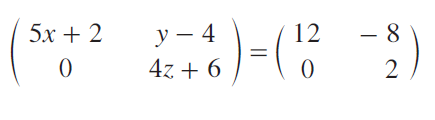
Solution :
The above matrices on both sides same order. So, the corresponding elements are equal.
5x + 2 = 12 -----(1)
y - 4 = -8 -----(2)
4z + 6 = 2 -----(3)
By solving (1), we get
|
5x + 2 = 12 5x = 12-2 5x = 10 x = 2 |
y - 4 = -8 y = -8+4 y = -4 |
4z + 6 = 2 4z = 6-2 4z = 4 z = -1 |
So, the values of x, y and z are 2, -4 and -1 respectively.
Question 2 :
Let
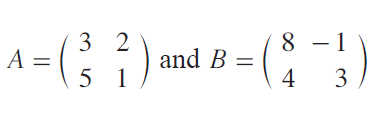
Find the matrix C if C = 2A + B
Solution :
To get the new matrix C, we should multiply the scalar 2 by matrix A and add it by the matrix B.
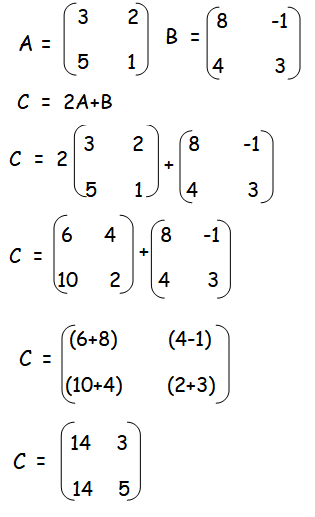
Question 3 :
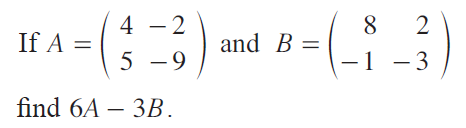
Solution :
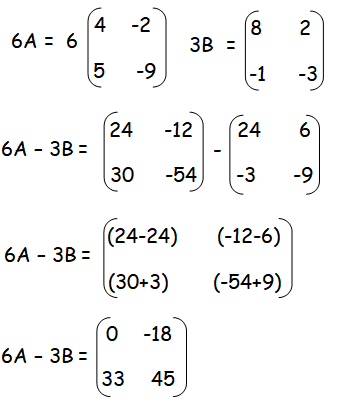
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4)
