MULTIPLYING RADICALS WITH DIFFERENT ROOTS WORKSHEET

Simplify :

(1)  √2 × √5

(2)  √7 × √7

(3)  3√3 × 2√2

(4)  √3 × √2 × 2√2

(5)  - 3√2 × (√2)³

(6)  (3√2)³ × (√3)³

(7)  (2√5) × (3√2)

(8)  √3 × √2 × 2√2

(9)  √3 × √11

(10)  √2 × √3 × √5

Write the following in the form k√2 . Then find the value of k.

(11)  √8      (12)  √18      (13)  √200     (14)  √288

Write the following in the form k√3. Then find the value of k.

(15)  √12    (16)  √27

Write the following in the form k√5. Then find the value of k.

(17)  √20    (18)  √45

19)  The perimeter of an equilateral triangle is 624 centimeters. The height of this triangle is k√3 centimeters, where k is a constant. What is the value of k?

20)  A right triangle has legs with lengths of 24 centimeters and 21 centimeters. If the length of this triangle’s hypotenuse, in centimeters, can be written in the form 3√d , where d is an integer, what is the value of d ?

21)  Square X has a side length of 12 centimeters. The perimeter of square Y is 2 times the perimeter of square X. What is the length, in centimeters, of one side of square Y?

A) 6     B) 10    C) 14    D) 24

Simplify :

Problem 1 :

√2 × √5

Solution :

=  √2 × √5

=  √(2 ⋅ 5)

=  √10

So, the answer is √10

Problem 2 :

√7 × √7

Solution :

=  √7 × √7

=  √(7 ⋅ 7)

=  √49

=  7

So, the answer is 7

Problem 3 :

3√3 × 2√2

Solution :

=  3√3 × 2√2

=  (3⋅2) [√(3⋅2)]

=  6√6

So, the answer is 6√6

Problem 4 :

√3 × √2 × 2√2

Solution :

=  √3 × √2 × 2√2

=  (2) [√(3 ⋅ 2 ⋅ 2)]

=  (2⋅2) √3

=  4√3

So, the answer is 4√3

Problem 5 :

- 3√2 × (√2)³

Solution :

By using radicals property,

We get,

=  - 3√2 × (√2)³

=  - 3√2 × √2³

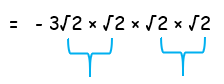
=  -3 (2 ⋅ 2)

=  - 12

So, the answer is - 12

Problem 6 :

(3√2)³ × (√3)³

Solution :

=  (3√2)³ × (√2)³

=  (3)³(√2³) × √2³

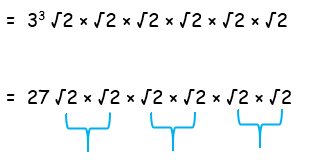
=  27 (2 ⋅ 2 ⋅ 2)

=  216

Problem 7 :

(2√5) × (3√2)

Solution :

=  (2√5) × (3√2)

=  (2⋅3)√(5⋅2)

=  6√10

So, the answer is 6√10.

Problem 8 :

√3 × √2 × 2√2

Solution :

=  √3 × √2 × 2√2

=  2 √(3⋅2⋅2)

=  (2⋅2)√3

=  4√3

So, the answer is 4√3.

Problem 9 :

√3 × √11

Solution :

=  √3 × √11

=  √(3⋅11)

=  √33

So, the answer is √33.

Problem 10 :

√2 × √3 × √5

Solution :

=  √2 × √3 × √5

=  √(2⋅3⋅5)

=  √30

So, the answer is √30.

Write the following in the form k√2 . Then find the value of k.

Problem 11 :

√8

Solution :

Given, √8

√8 it can be rewritten as √4 × √2

=  √4 × √2

=  2√2

So, the value of k is 2

Problem 12 :

√18

Solution :

Given, √18

√18 it can be rewritten as √9 × √2

=  √9 × √2

=  3√2

So, the value of k is 3

Problem 13 :

√200

Solution :

Given, √200

√200 it can be rewritten as √100 × √2

=  √100 × √2

=  10√2

So, the value of k is 10

Problem 14 :

√288

Solution :

Given, √288

√288 it can be rewritten as √144 × √2

=  √144 × √2

=  12√2

So, the value of k is 12.

Write the following in the form k√3. Then find the value of k.

Problem 15 :

√12

Solution :

Given, √12

√12 it can be rewritten as √4 × √3

=  √4 × √3

=  2√3

So, the value of k is 2.

Problem 16 :

√27

Solution :

Given, √27

√27 it can be rewritten as √9 × √3

=  √9 × √3

=  3√3

So, the value of k is 3

Write the following in the form k√5. Then find the value of k.

Problem 17 :

√20

Solution :

Given, √20

√20 it can be rewritten as √4 × √5

=  √4 × √5

=  2√5

So, the value of k is 2.

Problem 18 :

√45

Solution :

Given, √45

√45 it can be rewritten as √9 × √5

=  √9 × √5

=  3√5

So, the value of k is 3.

Problem 19 :

The perimeter of an equilateral triangle is 624 centimeters. The height of this triangle is k√3 centimeters, where k is a constant. What is the value of k?

Solution :

Perimeter of equilateral triangle = 624

Let x be the side of the equilateral triangle.

3x = 624

x = 624/3

= 208

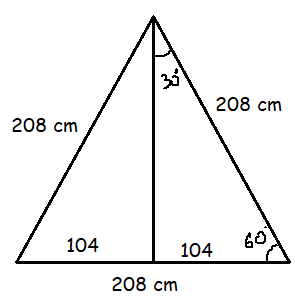
Base = 208 cm

In 30-60-90 right triangle, 

Smaller side = opposite of 30 degree = 104

2(smaller side) = 208

Longer side = opposite to 60 degree = √3smaller side

Height of the triangle = 104 √3

Comparing with given height k√3, the value of k is 104 cm.

Problem 20 :

A right triangle has legs with lengths of 24 centimeters and 21 centimeters. If the length of this triangle’s hypotenuse, in centimeters, can be written in the form 3√d , where d is an integer, what is the value of d ?

Solution :

Every right triangle should satisfy Pythagorean theorem,

24² + 21² = (3√d)²

576 + 441 = 9d

9d = 1017

d = 1017/9

d = 113

So, the required value of d is 113.

Problem 21 :

Square X has a side length of 12 centimeters. The perimeter of square Y is 2 times the perimeter of square X. What is the length, in centimeters, of one side of square Y?

A) 6     B) 10    C) 14    D) 24

Solution :

Side length of square X = 12 cm

Perimeter of square Y

= 2(Perimeter of square has side X)

Perimeter of square X = 4(12)

= 48 cm

Perimeter of square Y = 2(48)

= 96 cm

4a = 96

a = 96/4

= 24

Side length of square Y = 24 cm

So, option D is correct.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.