MULTIPLICATION AND DIVISION OF SURDS

About "Multiplication and division of surds" 

Multiplication and division of surds :

Here we are going to see the process of finding multiplication and division of surds.

How to multiply surds ?

Whenever we have two or more radical terms which are multiplied with same index, then we may put only one radical and multiply the terms inside the radical. 

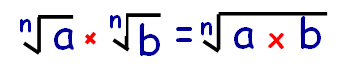
How to divide surds ?

Whenever we have two or more radical terms which are dividing with same index, then we can put only one radical and divide the terms inside the radical. 

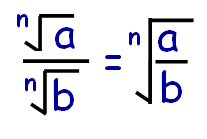
Let us look into some examples based on addition and subtraction of surds.

Example 1:

Simplify the following √5 ⋅  √18

Solution :

  =  √5 ⋅ √18

According to the laws of radical,

  =  √(5 ⋅ 18) 

   =  √(5 ⋅ 3 ⋅ 3 ⋅ 2) 

=  3 √(5 ⋅ 2)  

  =  3√10

Example 2 :

Simplify the following ∛13 ⋅ ∛5

Solution :

  =  ∛13 ⋅ ∛5

According to the laws of radical,

  =  ∛(13 ⋅ 5)  =  ∛65

Example 3 :

Simplify the following ∛7 ⋅ ∛8

Solution :

  =  ∛7 ⋅ ∛8

According to the laws of radical,

  = ∛(7 x 8) ==> ∛(7 ⋅ 2 ⋅ 2 ⋅ 2) ==> 2 ∛(7 ⋅ 2) ==> 2 ∛14

Example 4 :

Simplify the following ∜32 ⋅ ∜8

Solution :

  =  ∜32 ⋅ ∜8

=  ∜(32 ⋅ 8)

=  ∜(2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2)

=  (2 ⋅ 2)

  =  4

Example 5 :

Simplify the following 3√35 ÷ 2√7

Solution :

  =   3√35 ÷ 2√7

According to the laws of radical,

  =  (3/2) √(35/7) ==> (3/2)√5

Example 6 :

Simplify the following 15√54 ÷ 3√6

Solution :

  =   15√54 ÷ 3√6

According to the laws of radical,

  =  (15/3)√(54/6) 

=  (15/3)√9

  =  (15/3) ⋅ 3  =  15

Example 7 :

Simplify the following ∛128 ÷ ∛64

Solution :

  =   ∛128 ÷ ∛64

According to the laws of radical,

  =  ∛(128/64)

  =  ∛2

Example 8 :

Simplify the following ∜8 ⋅ ∜12

Solution :

  =  ∜8 ⋅ ∜12

According to the laws of radical,

  =  ∜(8/12)

=  ∜(2/3)

Example 9 :

Simplify the following 6∜16 ÷ ∜81

Solution :

  =  6∜16 ÷ ∜81

=  6∜(16/81)

=  6∜(2 ⋅ 2 ⋅ 2 ⋅ 2)/(3 ⋅ 3 ⋅ 3 ⋅ 3)

Since we have the order 4, we have to to factor one term for every four same terms.

=  6 ⋅ (2/3)

 =  2 ⋅ 2   

  =  4

Example 10 :

Simplify the following ∜256 ⋅ ∜81

Solution :

  =  ∜256 ⋅ ∜81

=  ∜(256 ⋅ 81)

=  ∜(4 ⋅ 4 ⋅ 4 ⋅ 4 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3)

=  4 ⋅ 3

  =  12

Related topics

• Rationalization of surds
• Comparison of surds
• Operations with radicals
• Ascending and descending  order of surds
• Simplifying radical expression
• Exponents and powers

We hope that the students would have understood the stuff given on "Multiplication and division of surds"

Apart from the stuff given above, if you want to know more about "Multiplication and division of surds"

If you need any other stuff, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.