ASCENDING AND DESCENDING ORDER OF SURDS

Irrational numbers with same order can be compared. If we want to compare irrational numbers with different orders, we have convert them with same order and compare. 

How to write irrational numbers (surds) in ascending order and descending order ?

(i)  Writing irrational numbers (surds) with same order from smaller to greater is known as 'ascending order'.

(ii) Writing irrational numbers(surds) with same order from greater to smaller is known as 'descending order'.

How to convert irrational numbers with different orders to irrational numbers with same order ?

(1) Write the orders of irrational numbers given.

(2) Find the least common multiple. 

(3) Make the order same using least common multiple found. 

(4) Now we can compare the radicands.

Solved Problems

Problem 1:

Write the irrational numbers √3, ³√2 and ⁴√4 in 

(i) ascending order

(ii) descending order

Solution:

Order of given irrational numbers are 2, 3 and 4.

Find the least common multiple 2, 3 and 4.  

Least common multiple of (2, 3 and 4)  =  12

Now, we have to change the order of each radical term as 12 as shown below. 

First, let change √3 as 12^th root. 

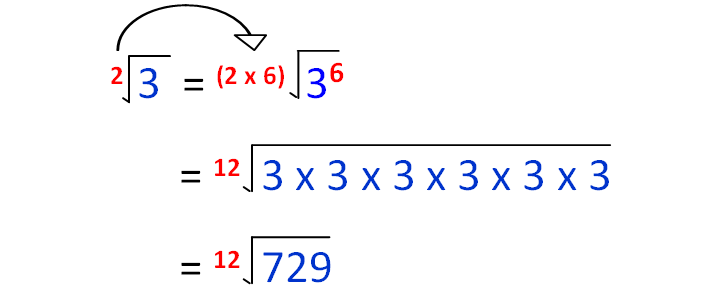
Now, let's change ³√2 as 12th root. 

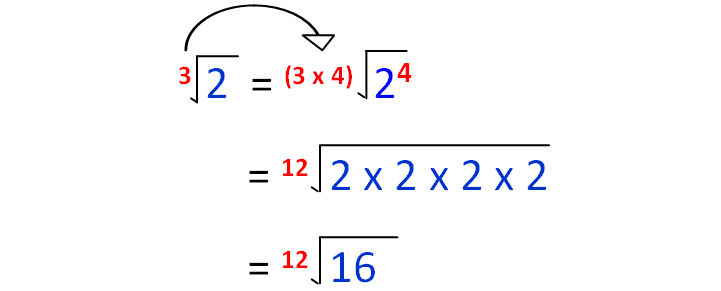
Now, let's change ⁴√4 as 12th root. 

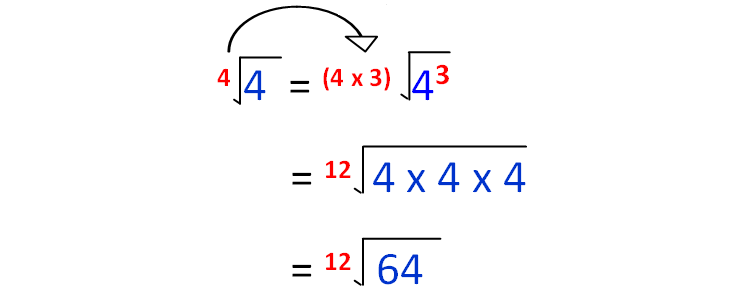
We have changed all the given radical terms with same order.

12th root (16) is the least number

12th root (64) is the next greater number

12th root (729) is the greatest number

Ascending Order :

To write the number in ascending order, we have to write them from least to greatest.  

³√2 < ⁴√4 < √3 

Descending Order :

Descending order means we have to write the number from least to greatest.

√3 > ⁴√4 > ³√2

Problem 2 :

Write the irrational numbers ⁴√5, √3 and ³√4 in 

(i) ascending order

(ii) descending order.

Solution :

Order of given irrational numbers are 4, 2 and 3.

Find the least common multiple 4, 2 and 3.  

Least common multiple of (4, 2 and 3)  =  12

Now, we have to change the order of each radical term as 12 as shown below. 

First, let change ⁴√5 as 12^th root. 

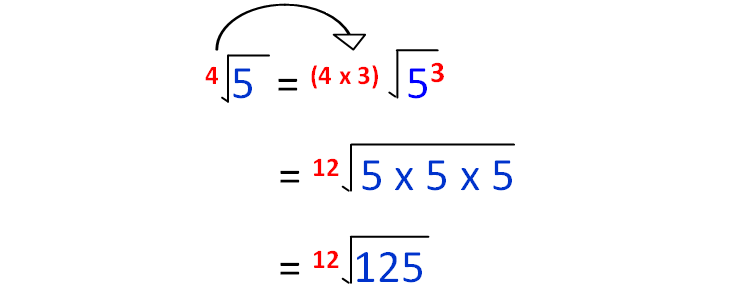
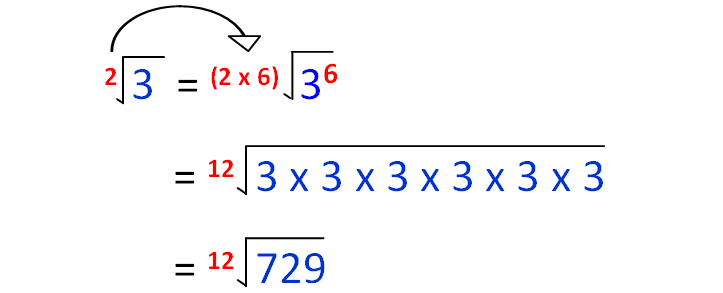
Now, let's change √3 as 12^th root. 

Now, let's change ³√4 as 12^th root. 

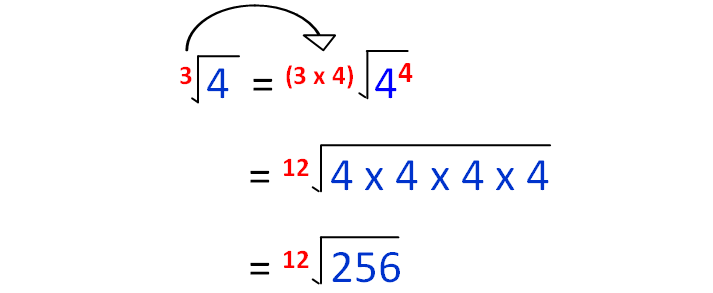
We have changed all the given radical terms with same order.

12th root (125) is the least number

12th root (256) is the next greater number

12th root (729) is the greatest number

Ascending Order :

Ascending order means we have to write the number from least to greatest.

√3 < ³√4 < ⁴√5

Descending Order :

Descending order means we have to write the number from greatest to least.

⁴√5 < ³√4 < √3

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.