OPERATIONS WITH RADICALS

Addition and Subtraction of Radicals

Addition and subtraction of two or more radical terms can be performed with like radicands only. 

Like radicand means a number which is inside root sign must be same but the number outside the radical may be different.

For example,

5√2 + 3√2 = 8√2

Here 5√2 and 3√2 are like radical terms.

Multiplying and Dividing Radicals

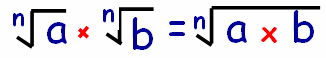
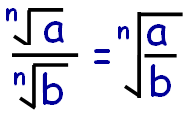
Whenever we have two or more radical terms which are multiplied with same index, then we can put only one radical and multiply the terms inside the radical. 

Whenever we have two or more radical terms which are dividing with same index, then we can put only one radical and divide the terms inside the radical. 

Problem 1 :

Simplify the following radical expression 

7√30 + 2√75 + 5√50 

Solution :

                    = 7 √30 + 2 √75 + 5 √50 

First we have to split the given numbers inside the radical as much as possible.

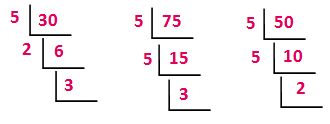
=  √(5 x 2 x 3) + √(5 x 5 x 3) + √(5 x 5 x 2)

Here we have to keep √30 as it is.

=  √30 + 5 √3 + 5 √2

Problem 2 :

Simplify the following √5 x √18

Solution :

  = √5 x √18

According to the laws of radical,

= √(5 x 18) ==> √(5 x 3 x 3)  ==> 3 √5

Problem 3 :

Simplify the following

∛7 x ∛8

Solution :

  =  ∛7 x ∛8

According to the laws of radical,

  = ∛(7 x 8) ==> ∛(7 x 2 x 2 x 2) ==> 2 ∛7 x 2 ==> 2 ∛14

Problem 4 :

Simplify the following 

3√35 ÷ 2√7

Solution :

  = 3√35 ÷ 2√7

According to the laws of radical,

  =  (3/2) √(35/7) ==> (3/2)√5

Problem 5 :

Which of the following is not a perfect square?

(a) 361     (b) 1156     (c) 1128    (d) 1681

Solution :

By observing perfect squares,

1, 4, 9, 16, 25, 36, 49, 64, 81, 100, ............

These are the perfect squares ends with the digits 0, 1, 4, 5, 6, 9. The perfect squares will not ends with 2, 3, 6, 7, 8

In option c, the unit digit is 8, it is not a perfect square.

Problem 6 :

A perfect square can never have the following digit at ones place.

(a) 1       (b) 6     (c) 5       (d) 3

Solution :

By observing the above perfect squares, the number ends with the digit 3 will not be a perfect square. So, option d is correct.

Problem 7 :

The value of √(176 + √2401)

Solution :

= √(176 + √2401)

Let us start with most interior bracket.

= √(176 + √(7 ⋅ 7 ⋅7 ⋅ 7)

= √(176 + (7 ⋅ 7)

= √(176 + 49)

= √225

= √(15 ⋅ 15)

= 15

Problem 8 :

Given that √5625 = 75, then the value of

 √0.5625 + √56.25

is

Solution :

√5625 = 75

√0.5625 = √0.5625(10000/10000)

= √(5625/10000)

= √(75 x 75/100 x 100)

= 75/100

= 0.75

√56.25 = √56.25(100/100)

= √(5625/100)

= √(75 x 75) / (10 x 10)

= 75/10

= 7.5

 √0.5625 + √56.25 = 0.75 + 7.5

= 8.25

Problem 9 :

The value of √248(√52 + (√144)) is

Solution :

= √(248 + (√52 + (√144)))

We start with most inner bracket

= √(248 + √(52 + (√12 ⋅ 12)))

= √(248 + √(52 + 12))

= √(248 + √64)

= √(248 + √(8 ⋅ 8)

= √(248 + 8)

= √256

= √16⋅16

= 16

So, the answer is 16.

Problem 10 :

Simplify 1/(2 - √3)

Solution :

= 1/(2 - √3)

To rationalize the denominator, we have to multiply both numerator and denominator by its conjugate.

= [1/(2 - √3)] ⋅ [(2 + √3) / (2 - √3)]

= (2 + √3) / (2 - √3) (2 + √3)

= (2 + √3) / (2² - √3²)

= (2 + √3) / (4 - 3)

= 2 + √3

Problem 11 :

Simplify (6 - √2)(√3 + 1)

Solution :

= (6 - √2)(√3 + 1)

Using distributive property, 

= 6√3 + 6(1) - √2√3 - √2(1)

= 6√3 + 6 - √6 - √2

Since we dont have any like terms, it cannot be simplified further. So, the answer is 6√3 + 6 - √6 - √2

Problem 12 :

Simplify √50 - √18 + √8

Solution :

=  √50 - √18 + √8

=  √2 ⋅ 5 ⋅ 5 - √2 ⋅ 3 ⋅ 3 + √2 ⋅ 2 ⋅ 2

=  5√2 - 3√2 + 2√2

=  5√2 + 2√2 - 3√2

=  7√2 - 3√2

=  4√2

Problem 13 :

Simplify √6 - (√2/√3) + (√3/√2)

Solution :

= √6 - (√2/√3) + (√3/√2)

To rationalize the denominator of √2/√3, we have to multiply both numerator and denominator by √3

= (√2/√3) ⋅ (√3/√3)

= √6/3

To rationalize the denominator of √3/√2, we have to multiply both numerator and denominator by √2

= (√3/√2) ⋅ (√2/√2)

= √6/2

Applying these values, we get

= √6 - (√6/3) + (√6/2)

= (6√6 - 2√6 + 3√6)/6

= 7√6/6

Problem 14 :

Solve the equation √(5 - 2x) = 3

Solution :

√(5 - 2x) = 3

To solve the radical equation, we have to use square on both sides.

(5 - 2x) = 3²

5 - 2x = 9

2x = 5 - 9

2x = -4

x = -4/2

x = -2

Problem 15 :

Solve the equation √-5 √-10

Solution :

= √-5 √-10

= √-5(-10)

= √50

= √(2⋅5⋅5)

= 5√2

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.