MAXIMUM OR MINIMUM VALUE OF A QUADRATIC FUNCTION

We can determine the maxim or minimum value of the quadratic function using the vertex of the parabola (graph the quadratic function).

The general form of a quadratic function is 

f(x)  =  ax² + bx + c

Here, if the leading coefficient or the sign of "a" is positive, then the graph of the quadratic function will be a parabola which opens up. 

If the leading coefficient or the sign of "a" is negative, then the graph of the quadratic function will be a parabola which opens down. 

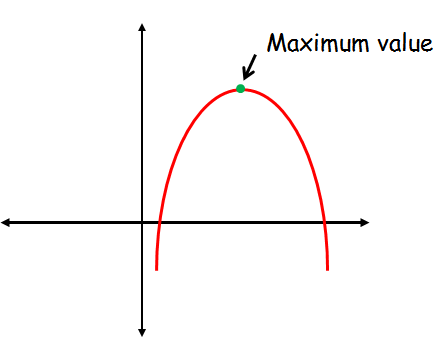
Maximum Value of a Quadratic Function

The quadratic function f(x)  =  ax² + bx + c will have only the maximum value when the the leading coefficient or the sign of "a" is negative.

When "a" is negative the graph of the quadratic function will be a parabola which opens down. 

The maximum value is "y" coordinate at the vertex of the parabola.  

Note :

There is no minimum value for the parabola which opens down. 

Minimum Value of a Quadratic Function

The quadratic function f(x)  =  ax² + bx + c will have only the minimum value when the the leading coefficient or the sign of "a" is positive.

When "a" is positive, the graph of the quadratic function will be a parabola which opens up. 

The minimum value is "y" coordinate at the vertex of the parabola.  

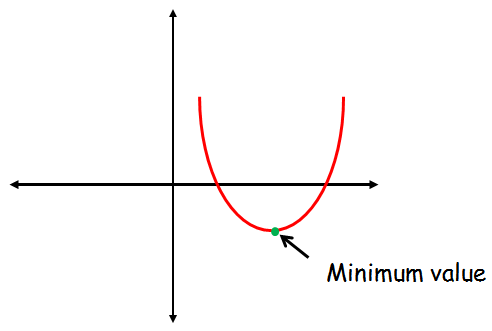
Note :

There is no maximum value for the parabola which opens up. 

Vertex of a Parabola

To find the vertex of the parabola which is given by the quadratic function

f(x)  =  ax² + bx + c,

we have to substitute 

x  =  -b/2a

And the vertex is 

[-b/2a, f(-b/2a)]

So, the maximum or minimum value of the quadratic function is, 

"y" coordinate  =  f(-b/2a)

Examples

Example 1 : 

Find the minimum or maximum value of the quadratic equation given below. 

f(x)  =  2x² + 7x + 5

Solution : 

In the given quadratic function, since the leading coefficient (2x²) is positive, the function will have only the minimum value. 

When we compare the given quadratic function with

f(x)  =  ax² + bx + c,

we get 

a  =  2

b  =  7

c  =  5

"x" coordinate of the vertex  =  -b/2a

"x" coordinate of the vertex  =  -7/2(2)

"x" coordinate of the vertex  =  -7/4

"x" coordinate of the vertex  =  -1.75

Minimum value  is 

=  f(-1.75)

=  2(-1.75)² + 7(-1.75) + 5

=  2(3.0625) - 12.25 + 5

=  6.125 - 12.25 + 5

=  -1.125

So, the minimum value of the given quadratic function is -1.125. 

Example 2 : 

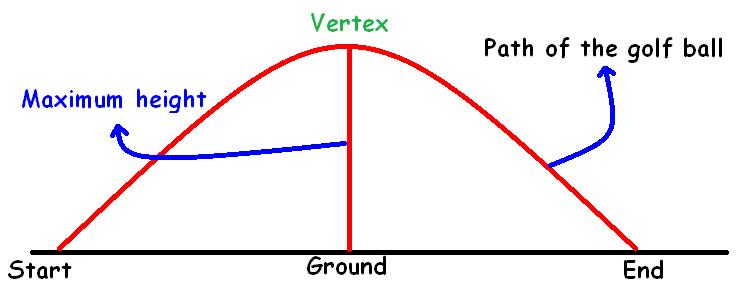
A golfer attempts to hit a golf ball over a gorge from a platform above the ground. The function that models the height of the ball is 

h(t)  =  -5t² + 40t + 100

where 'h' is the height in meters 't' is time in seconds after contact. Find the maximum height reached by the golf ball.

Solution : 

It is clear that the path of the golf ball is a parabola which opens up.

It has been illustrated in the picture given below.

When we compare the given quadratic function with

f(x)  =  ax² + bx + c,

we get 

a  =  -5

b  =  40

c  =  100

"x" coordinate of the vertex  =  -b / 2a

"x" coordinate of the vertex  =  -40 / 2x(-5)

"x" coordinate of the vertex  =  -40 / (-10)

"x" coordinate of the vertex  =  4

Maximum height is 

=  h(4)

=  -5(4)² + 40(4) + 100

=  -5(16) + 160 + 100

=  -80 + 160 + 100

=  180

So, the maximum height reached by the golf ball is 180 meters.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.