MATH OLYMPIAD SAMPLE PROBLEMS 6TH GRADE

Question 1 :

5/7 of number A is the same as 1/4 of number B. What is the minimum sum of numbers A and B ?

Solution :

5/7 of A  =  1/4 of B

5A/7  =  B/4

5A  =  7B/4

A  =  7B/20

A + B  =  (7B/20) + B

  =  (7B + 20B)/20

A + B  =  27B/20  

When B  =  20

A + B  =  (27/20) ⋅ 20

A + B =  27

Question 2 :

The four corners of a a square piece of paper of side 18 cm are cut off as shown below. The piece of paper is then folded along the dotted lines into a tray. What must be the length of each of four small squares so that the volume of the tray is maximum ? (Consider only whole numbers.)

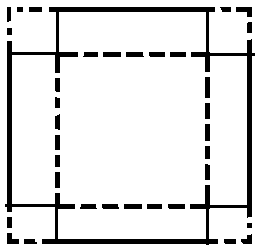
Solution :

Let x be the side length of the small square.

By folding the given shape along the dotted line, we will get a cuboidical  tray.

If length of the square is 1 cm, then

Dimension of tray :

length  =  16, width  =  16 and height  =  1

Volume of the tray  =  l ⋅ b ⋅ h

Volume  =  16 ⋅ 16 ⋅ 1

  =  256 cm²

If length of the square is 2 cm, then

Dimension of tray :

length  =  14, width  =  14 and height  =  2

Volume  =  14 ⋅ 14 ⋅ 2

  =  392 cm²

If length of the square is 3 cm, then

Dimension of tray :

length  =  12, width  =  12 and height  =  3

 Volume  =  12 ⋅ 12 ⋅ 3

  =  432 cm²

If length of the square is 4 cm, then

Dimension of tray :

length  =  10, width  =  10 and height  =  4

 Volume  =  10 ⋅ 10 ⋅ 4

  =  400 cm²

If length of the square is 5 cm, then

Dimension of tray :

length  =  8, width  =  8 and height  =  5

 Volume  =  8 ⋅ 8 ⋅ 5

  =  320 cm²

So, the length of each of the four small squares must be 3 cm so that the volume of the tray is the maximum.

Question 3 :

Compute the sum of all odd numbers smaller than 100.

Solution :

By writing the odd numbers lesser than 100 as series, we get

1 + 3 + 5 + 7 +................... + 99

To find the sum of odd numbers, we have a formula. 

  =  n²  (or) [(l + 1)/2]²

Let us use the second formula to find the sum of odd numbers.

  =  [(99 + 1)/2]²

  =  50²

  =  2500

Question 4 :

Two goods train each 500 m long are running in opposite directions on parallel tracks. Their speeds are 45 km/hr and 30 km/hr respectively. Find the time taken by the slower train to pass the faster train.

Solution : 

Two trains are travelling in opposite direction.

Relative speed  =  Speed of 1^st train + speed of 2^nd train

  =  45 + 30

  =  75 km/hr

Converting km/hr to m/sec, we get

  =  75 ⋅ (5/18)

  =  375/18

Here slower train has to pass faster train. 

Time taken  =  Distance / Relative Speed

Distance  =  length of train

  =  500 / (375/18)

  =  24 seconds

Related topics

• Find the time taken by the train to pass a man
• Find the time taken by a train to pass a bridge or tunnel
• Train passes a moving object in the same direction
• Problems on finding the length of the train
• Finding the average speed of the round trip
• Finding the Speed When the Distance Traveled is Same 
  
• Two Cars Traveling Same Direction Different Speeds
  
• Two cars traveling in opposite direction

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.