TWO CARS TRAVELLING IN OPPOSITE DIRECTIONS

Two Cars Travelling in Opposite Directions :

In this section, we will learn how to solve problems based on two cars travelling in opposite directions.

The relationship between distance, speed and time.

Time  =  Distance / Speed 

Speed  =  Distance / Time

Distance  =  Time ⋅ Speed

To convert minutes into hour, we should divide the given minutes by 60.

• If we want to convert the speed from km/hr to m/sec, we should multiply the speed by 5/18.
• If we want to convert the speed from m/sec to km/hr, we should multiply the speed by 18/5.

Example 1 :

Town A and Town B are 420 km apart. A car leaves Town A for Town B and another car leaves Town B for Town A. If car A has a head start of 2.5 hours, the two cars will pass each other 2.5 hours after car B starts its journey. If car B has a head start of 2 hours, the two cars will pass each other 3 hours after car A starts its journey. Find their respective speeds.

Solution :

Let x and y be the speed of car A and car B respectively.

What is head start ?

When a runner allows to start the race 'x' meters ahead from the starting point , then we can say that the runner got a head start of (start up) x meters.

If the runner allows starting the race by 't' seconds earlier than the other runners, then the runner got a head start of t seconds.

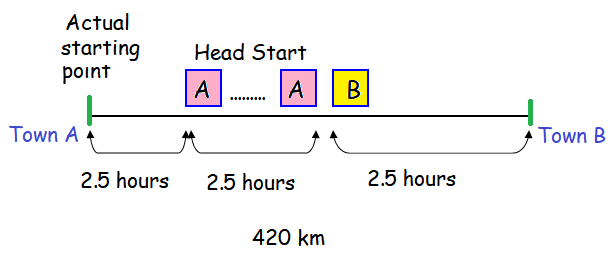
Time taken by car A to meet car B is 5 hours. At the meeting point, car B has traveled 2.5 hours.

5x + 2.5y  =  420  -------(1)

Time taken by car B to meet car A is 5 hours. At the meeting point, car B has traveled 5 hours and car A has traveled 3 hours.

3x + 5y  =  420  -------(2)

(1) ⋅ 2 ==>  10x + 5y  =  840  -----(3)

(3) - (2)

10x - 3x  =  840 - 420

7x  =  420

x  =  420/7

x  =  60

By applying the value of x in (2), we get

3(60) + 5y  =  420

180 + 5y  =  420

5y  =  420 - 180

5y  =  240

y  =  48

The speed of car A and car B are 60 km/hr and 48 km/hr respectively.

Related topics

• Find the time taken by the train to pass a man
• Find the time taken by a train to pass a bridge or tunnel
• Train passes a moving object in the same direction
• Problems on finding the length of the train
• Finding the average speed of the round trip
• Finding the Speed When the Distance Traveled is Same 
  
• Two Cars Traveling Same Direction Different Speeds
  

Apart from the stuff given on this web page, if you need any other stuff in math, please use our google custom search here

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.