LINEAR SYSTEMS WORKSHEET

Problem 1 :

Find the solution of the system of linear equations and justify your answer. 

x + 2y  =  3

x - 2y  =  4

Problem 2 :

John earns $20 per hour mowing lawns and $10 per hour walking dogs. His goal is to earn at least $200 per week, but he can work a maximum of 20 hours per week. John must spend at least 5 hours per hours walking his neighbor's dogs. For how many hours should John work at each job in order to meet his goals ?   

Problem 3 :

A trader has 100 units of a product. He sells some of the units at $6 per unit and the remaining units at $8 per units. He receives a total of $660 for all 100 units. Find the number units sold in each category. 

Problem 4 :

To secure A grade one must obtain an average of 90 marks or more in 5 subjects each of maximum 100 marks. If one scored 84, 87, 95, 91 in first four subjects, what is the minimum mark one scored in the fifth subject to get A grade in the course ?

Linear Systems Worksheet - Solutions

Problem 1 :

Find the solution of the system of linear equations and Justify your answer. 

x + 2y  =  3

x - 2y  =  4

Solution :

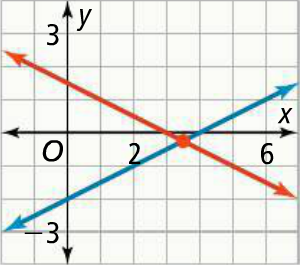
Sketch the graph of each equation to estimate the solutions. Then solve algebraically. 

To graph each equation, write the equations in slope intercept form. 

x + 2y  =  3 -----> y  =  (-1/2)x + 3/2 ----> (1)

x - 2y  =  4 -----> y  =  (1/2)x - 2 ----> (2)

For the first equation, the slope is -1/2 and y-intercept is 3/2 or 1.5

For the second equation, the slope is 1/2 and y-intercept is -2.

Graph : 

Solve the equations algebraically : 

x + 2y  =  3 -----> x  =  3 - 2y ---- (A)  

x - 2y  =  4 -----> x  =  4 + 2y ----(B)

From (A) and (B), we have

x  =  x

3 - 2y  =  4 + 2y

- 1  =  4y

- 1/4  =  y

Plug y  =  - 1/4 in (A).

x  =  3 - 2(-1/4)

x  =  3 + 1/2

x  =  7/2

Hence, the solution to the given system of linear equations is 

(7/2, -1/4)

Justification :

In the graph above, the x-coordinate of the solution is between 3 and 4, and the y-coordinate of the solution is between -1 and 0. 

The values 7/2 and -1/4 in the solution are close to the estimate made from the graph.

So, the solution (7/2, -1/4) is reasonable. 

Problem 2 :

John earns $20 per hour mowing lawns and $10 per hour walking dogs. His goal is to earn at least $200 per week, but he can work a maximum of 20 hours per week. John must spend at least 5 hours per hours walking his neighbor's dogs. For how many hours should John work at each job in order to meet his goals ?   

Solution : 

Step 1 : 

Define the variables. 

x  =  Number of hours spent mowing lawns 

y  =  Number of hours spent walking dogs

Step 2 :

Write inequalities to model the constraints. 

John wants to earn at least $200 each week at $20 per hour mowing lawns and $10 per hour walking dogs : 

20x + 10y  ≥  200

John cannot work more than 20 hours each week : 

x + y  ≤  20

John must spend at least 5 hours walking dogs each week :

y  ≥  5

Step 3 :

Solve each inequality for y, then graph the inequalities on the same coordinate plane. 

20x + 10y  ≥  200 -----> y  ≥  20 - 2x

x + y  ≤  20 -----> y  ≤  20 - x

y  ≥  5 -----> y  ≥  5

Use arrows to show the region of the graph that satisfies each inequality. 

Shade region that satisfies all three inequalities. 

Graph :

Any point in the shaded region, such as (12, 7), is a solution to the system of inequalities.

That is, if John spends 12 hours mowing lawns 7 hours walking dogs, he will meet the his goal of earning at least $200 per week.     

Problem 3 :

A trader has 100 units of a product. He sells some of the units at $6 per unit and the remaining units at $8 per units. He receives a total of $660 for all 100 units. Find the number units sold in each category. 

Solution :

Let x be the no. of units sold at $6/unit and y be the no. of units sold at $8/unit.

Given : The trader sells 100 units in all. 

So, we have 

x + y  =  100 ------(1)

Given : He receives a total of $660 for all 100 units.

So, we have 

6x + 8y  =  660

Divide both sides by 2.

3x + 4y  =  330 ------(2)

Solving (1) and (2), we get

x  =  70 and y  =  30

Hence, the no. of tickets sold at $6 per unit is 70 and the no. of tickets sold at $8 per unit is 30.

Problem 4 :

To secure A grade one must obtain an average of 90 marks or more in 5 subjects each of maximum 100 marks. If one scored 84, 87, 95, 91 in first four subjects, what is the minimum mark one scored in the fifth subject to get A grade in the course ?

Solution :

Let "x" be the required mark in fifth subject

Four subjects marks are 84, 87, 95 and 91

The average of five subject marks would be grater than or equal to 90

(84 + 87 + 95 + 91 + x)/5  ≥ 90

Multiply by 5 on both sides

357 + x  ≥  90(5)

357 + x  ≥  450

Subtract both sides by 357

x  ≥ 450 - 357

x  ≥ 93

Hence the minimum mark is 93.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.