LINEAR INEQUALITIES

Identifying Solutions of Inequalities

Tell whether the ordered pair is a solution of the inequality.

Example 1 : 

(7, 3) ; y < x - 1

Solution :

Substitute 7 for x and 3 for y in the given inequality. 

3 < 7 - 1

3 < 4 ✓

(7, 3) is a solution.

Example 2 : 

(4, 5) ; y > 3x + 2

Solution :

Substitute 4 for x and 5 for y in the given inequality. 

5 > 3(4) + 2

5 > 12 + 2

 5 > 14 ✗

(4, 5) is not a solution.

Graphical Solution of Linear Inequalities

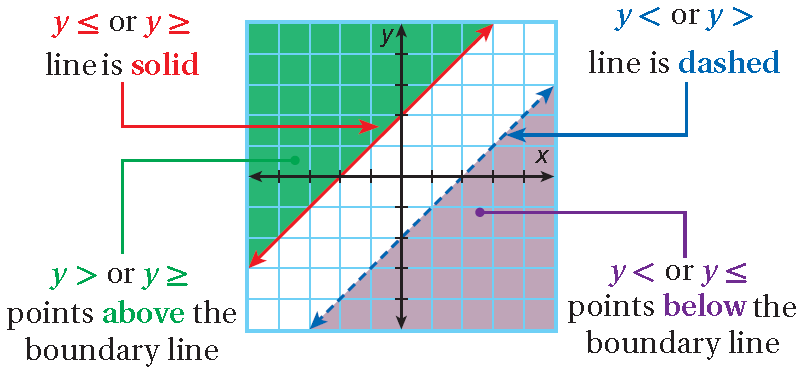
1. When the inequality is written as y ≤ or y ≥, the points on the boundary line are solutions of the inequality, and the line is solid.

2. When the inequality is written as y > or y ≥, the points above the boundary line are solutions of the inequality.

3. When the inequality is written as y < or y >, the points on the boundary line are not solutions of the inequality, and the line is dashed.

4. When the inequality is written as y < or y ≤, the points below the boundary line are solutions of the inequality.

Graphing Linear Inequalities in Two Variables

Graph the solutions of each linear inequality.

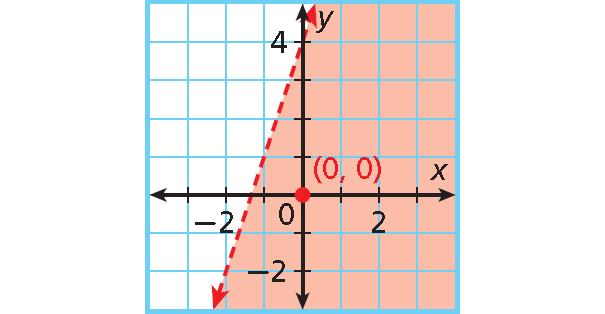
Example 3 : 

y < 3x + 4

Solution : 

Step 1 : 

The inequality is already solved for y.

Step 2 : 

Graph the boundary line y = 3x + 4. Use a dashed line for <.

Step 3 : 

The inequality is <, so shade below the line.

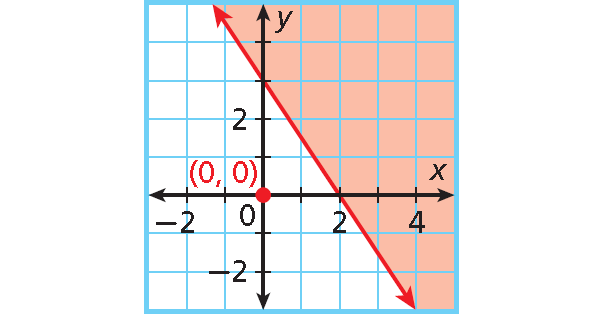
Example 4 : 

3x + 2y ≥ 6

Solution : 

Step 1 : 

Solve the inequality for y.

3x + 2y  ≥  6

2y  ≥  6 - 3x

y  ≥  3 - (3/2)x

y  ≥  -(3/2)x + 3

Step 2 : 

Graph the boundary line y = -(3/2)x + 3. Use a solid line for ≥.

Step 3 : 

The inequality is ≥, so shade above the line.

Writing an Inequality from a Graph

Write an inequality to represent each graph.

Example 5 : 

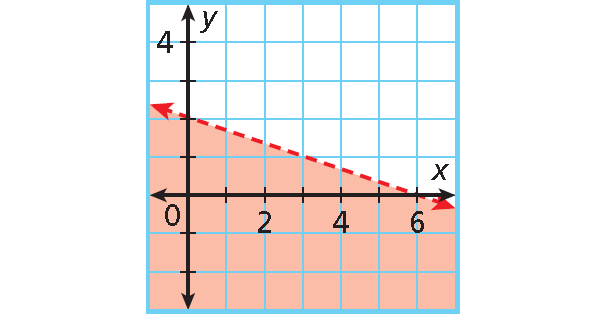
Solution : 

y-intercept : 2; slope : - 1/3.

Write an equation in slope-intercept form.

y = mx + b ---> y = -(1/3)x + 2

The graph is shaded below a dashed boundary line.

Replace = with < to write the inequality y < -(1/3)x + 2.

Example 6 :

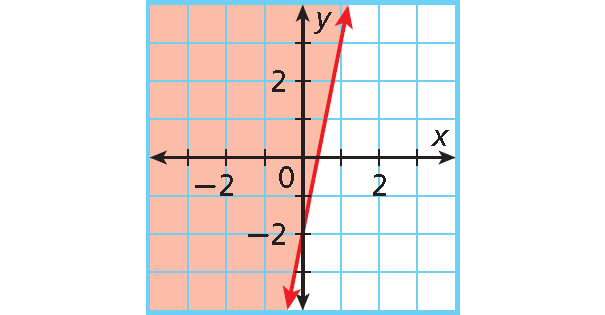
Solution : 

y-intercept : -2; slope : 5.

Write an equation in slope-intercept form.

y = mx + b ---> y = 5x + (-2)

The graph is shaded above a solid boundary line.

Replace = with ≥ to write the inequality y ≥ 5x - 2.

Example 7 :

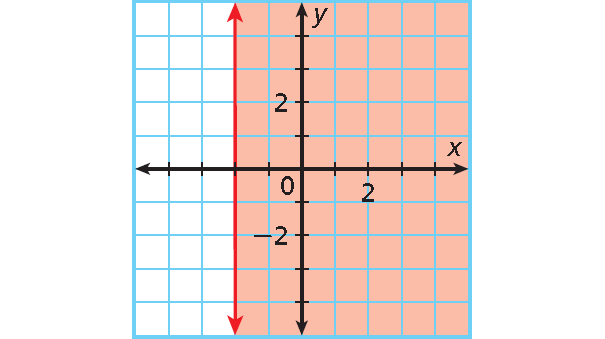
Solution : 

y-intercept : none; slope : undefined.

The graph is a vertical line at x = -2.

The graph is shaded on the right side of a solid boundary line.

Replace = with ≥ to write the inequality x ≥ - 2.

Consumer Economics Application

Example 8 :

Lily can spend at most $7.50 on vegetables for a party. Broccoli costs $1.25 per bunch and carrots cost $0.75 per package.

A. Write a linear inequality to describe the situation.

B. Graph the solutions.

C. Give two combinations of vegetables that Sarah can buy.

Solution : 

A. Write a linear inequality to describe the situation.

Let x represent the number of bunches of broccoli and let y represent the number of packages of carrots.

Write an inequality. Use ≤ for “at most.”

Cost of broccoli plus cost of carrots is at most $7.50

1.25x + 0.75y ≤ $7.50

Solve the inequality for y.

1.25x + 0.75y  ≤  7.50

100(1.25x + 0.75y)  ≤  100(7.50)

125x + 75y  ≤  750

75y  ≤  750 - 125x

75y/75  ≤  750/75 - 125x/75

y  ≤  10 - (5/3)x

y  ≤  -(5/3)x + 10

B. Write a linear inequality to describe the situation.

Step 1 : 

Because Lily cannot buy a negative amount of vegetables, the system is graphed only in Quadrant I. Graph the boundary line y = -(5/3)x + 10. Use a solid line for ≤.

Step 2 :

Shade below the line. Lily must buy whole numbers of bunches or packages. All points on or below the line with whole-number coordinates represent combinations of broccoli and carrots that Lily can buy.

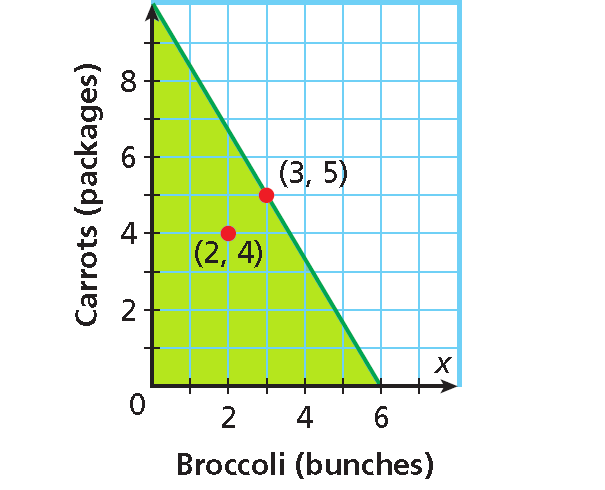
C. Give two combinations of vegetables that Lily can buy.

Two different combinations that Lily could buy for $7.50 or less are 2 bunches of broccoli and 4 packages of carrots, or 3 bunches of broccoli and 5 packages of carrots.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.