INVERSE METHOD 3X3 MATRIX
In this page inverse method 3x3 matrix we are going to see how to solve the given linear equation using inversion method.
Formula:
This is the formula that we are going to use to solve any linear equations.
X = A-1 B
Example 1 :
Solve the following linear equation by inversion method
2x - y + 3z = 9
x + y + z = 6
x - y + z = 2
Solution :
First we have to write the given equation in the form AX = B. Here X represents the unknown variables. A represent coefficient of the variables and B represents constants.inverse method 3x3 matrix
|
|
|
To solve this, we have to apply the formula X = A-1B
|
|A| |
|
|
= 2 |
|
+1 |
|
+3 |
|
= 2 [1 + 1] + 1 [1 - 1] + 3 [-1 - 1]
= 2 [2] + 1 [0] + 3 [-2]
= 4 + 0 -6
= - 2 ≠ 0
Since A is a non singular matrix. A-1 exists.
|
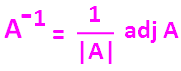
minor of 2 |
|
|||||||||||
|
= 1 - (-1) = 1 + 1 = 2 |
|
minor of -1 |
|
|||||||||||
|
= 1 - 1 = 0 |
|
minor of 3 |
|
|||||||||||
|
= -1 - 1 = -2 |
|
minor of 1 |
|
|||||||||||
|
inverse method 3x3 matrix |
= -1 - (-3) = -1 + 3 = 2 |
|
minor of 1 |
|
|||||||||||
|
inverse method 3x3 matrix |
= 2 - 3 = -1 |
|
minor of 1 |
|
|||||||||||
|
inverse method 3x3 matrix |
= -2 - (-1) = -2 + 1 = -1 |
|
minor of 1 |
|
|||||||||||
|
= -1 - 3 = -4 inversion method in3x3 matrices |
|
minor of -1 |
|
|||||||||||
|
= 2 - 3 = -1 |
|
minor of 1 |
|
|||||||||||
|
= 2 - (-1) = 2 + 1 = 3 |
|
minor matrix = |
|
||||||||||||||||||||
|
cofactor matrix = |
|
||||||||||||||||||||
|
Adj A = |
|
|
A-1 = 1/2 |
|
X = A-1B
|
= |
|
| = |
|
x |
|
|
x |
|
|
x |
|
|
| |||||||||||||||||
|
| |||||||||||||||||
|
|
So, the solutions are x = 1, y = 2 and z = 3
|
Practice Questions : | |
|
1) Solve the following homogeneous system of linear equations using inversion method |
2x + y + z = 5 x + y + z = 4 x - y + 2z = 1 |
|
2) Solve the following homogeneous system of linear equations using inversion method |
x + 2y + z = 7 2x - y + 2z = 4 x + y - 2z = -1 |
|
3) Solve the following homogeneous system of linear equations using inversion method |
x + y + z = 4 x - y + z = 2 2x + y - z = 1 |
|
4) Solve the following homogeneous system of linear equations using inversion method |
2x + 5y + 7z = 52 x + y + z = 9 2x + y - z = 0 |
|
5) Solve the following homogeneous system of linear equations using inversion method |
3x + y - z = 2 2x - y + 2z = 6 2x + y - 2z = -2 |
Related pages
- Types of matrices
- Equality of matrices
- Operation on matrices
- Algebraic properties of matrices
- Addition properties
- Determinant of matrix
- Adjoint of matrix
- Solving linear equations of two unknowns by cramer method
- Solving linear equations of three unknowns by cramer method
- Rank of matrix
- Linear dependence of vector
- Characteristic Equation of Matrix
- Characteristic Vector of Matrix
- Diagonalization of Matrix
- Gauss Elimination Method
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Permutation and Combination Problems
Nov 27, 22 08:59 PM
Permutation and Combination Problems -
Combination Problems With Solutions
Nov 27, 22 08:56 PM
Combination Problems With Solutions -
Like and Unlike Fractions Definition
Nov 26, 22 08:22 PM
Like and Unlike Fractions Definition - Concept - Examples with step by step explanation