IDENTIFY THE TERMS AND COEFFICIENTS IN AN ALGEBRAIC EXPRESSION

A single variable or a constant or a combination of these as a product or quotient forms a term.

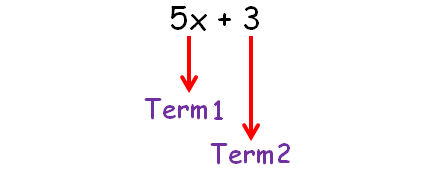
Terms can be added or subtracted to form an expression. In the expression 5x + 3 the term 5x is made of 2 factors and 5 and x while 3 is a single factor.

A numerical or constant quantity placed before and multiplying the variable in an algebraic expression

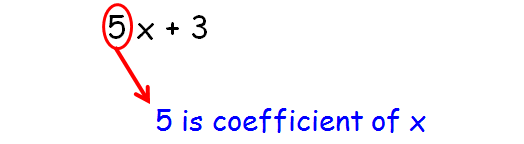
Identify the number of terms and coefficient of each term in the following expressions.

Example 1 :

2x⁵ + 3x³ - 12x² + 11x - 5

Solution :

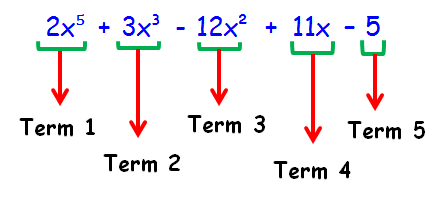
Terms :

There are five terms in the above algebraic expressions.

Term 1 = 2x⁵

Term 2 = 3x³

Term 3 = -12x²

Term 4 = 11 x

Term 5 = -5

Coefficients :

Coefficient of x⁵ = 2

Coefficient of x³ = 3

Coefficient of x² = -2

Coefficient of x = 11

Constant term = -5

Example 2 :

3x³ + x² - 2

Solution :

Terms :

There are three terms in the above algebraic expression.

Term 1 = 3x³

Term 2 = x² 

Term 3 = -2

Coefficients :

Coefficient of x³ = 3

Coefficient of x² = 1

Constant term = -2 

Example 3 :

5x + 10

Solution :

Terms :

There are two terms in the above algebraic expression.

Term 1 = 5x

Term 2 = 10

Coefficients :

Coefficient of x = 5

Constant term = 10 

Example 4 :

3xy - 7x

Solution :

Terms :

There are two terms in the above algebraic expression.

Term 1 = 3xy

Term 2 = -7x

Coefficients :

Coefficient of xy = 3

Coefficient of x = -7

Example 5 :

x/3 - 7y + 8

Solution :

Terms :

There are three terms in the above algebraic expression.

Term 1 = x/3

Term 2 = -7y

Term 3 = 8

Coefficients :

Coefficient of x = 1/3

Coefficient of y = -7

Constant = 8

Example 6 :

Identify the terms, coefficients, and constants in the expression.

Solution :

a)  7h + 3

• Terms : 7h and 3
• Coefficient of h is 7
• Constant is 3

b) g + 12 + 9g

10g + 12

• Terms : 10g and 12
• Coefficient of g is 10
• Constant is 12

c) 5c² + 7d

• Terms : 5c² and 7d
• Coefficient of c² is 5 and coefficient of d is 7.
• No constant

d) 2m² + 15 + 2p²

• Terms : 2m², 2p² and 15.
• Coefficient of m² is 2 and coefficient of p² is 2.
• Constant is 15.

e)  6 + m² + (1/2)d

• Terms : (1/2)d, m² and 6.
• Coefficient of m² is 1 and coefficient of d is 1/2.
• Constant is 6.

f)  8x + (x²/3)

• Terms : x²/3 and 8x
• Coefficient of x² is 1/3 and coefficient of x is 8.
• No constant

Example 5 :

Describe and correct the error in identifying the terms, coefficients, and constants in the algebraic expression 2x²y.

Solution :

The given term is 2x²y.

• There is only one term
• Coefficient of x²y is 2.
• There is no constant.

Example 6 :

You can use the expression 2ℓ + 2w to find the perimeter of a rectangle where ℓ is the length and w is the width.

a. Identify the terms, coefficients, and constants in the expression.

b. Interpret the coefficients of the terms.

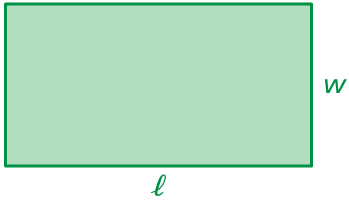
Solution :

Perimeter of the rectangle is given that = 2l + 2w

a) There are two terms, they are 2l and 2w.

Coefficients are 2 and 2.

There is no constant.

b) Adding length (l) two times and width (w) two times, we get the perimeter of the rectangle.

Example 7 :

Write an expression containing x-terms and constants. The x-terms should combine to 7x and the constants should sum to 13.

Solution :

The sum of 7x and 13 is 7x + 13.

Example 8 :

Write an expression containing x²-terms, x-terms and constants. The x²-terms should combine to −2x² the x-terms should subtract to 3x, and the constants should sum to 3.

Solution :

The required expression is 

−2x² + 3x + 3

Example 9 :

Each runner is carrying an 8-ounce bottle of water, a 2.1- ounce energy bar, and a 3-ounce energy drink. Write an expression in simplest form that represents the weight carried by y runners. Interpret the expression

Solution :

Let b be the water bottle, e be energy bar and d be energy drink.

Let y be the weight carried by runners y.

y = 8b + 2.1e + 3d

Example 10 :

Identify the terms, variables, coefficients, and constant of the SIMPLIFIED expression.

5x³ – 7x – 12x³ – 8x + 3

a) Simplified Expression:

b) Number of Terms:

c) Coefficients:

d) Variables:

e) Leading Coefficient:

f) Constant:

g) Degree:

h) Classify by degree:

Solution :

a)

5x³ – 7x – 12x³ – 8x + 3

By combining the like terms 

= 5x³ – 12x³ – 7x  – 8x + 3

= – 7x³ – 15x + 3

b)  There are three terms.

c)  Coefficients :

Coefficient of x³ is -7

Coefficient of x is -15

d) Variable is x

e) Leading Coefficient is -7

f) Constant is 3

g) Degree of the polynomial is 3

h) Cubic polynomial. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.