HOW TO FIND THE DOMAIN AND RANGE OF A FUNCTION

Domain :

Let y  =  f(x) be a function.

Domain is all real values of x for which y is defined.

If there is any value of x for which y is undefined, we have to exclude that particular value from the set of domain. 

For example, let us consider the function

f(x)  =  (3x - 2)/(x² - 1)

The above function accepts all real values except -1 and 1.If we apply x = 1 and -1, the function will become meaningless.

So, the domain of the given function is R - {-1, 1}

Range :

Let y  =  f(x) be a function.

Range is all real values of y for the given domain (real values of x). 

Let us look at some examples to understand how to find domain and range of a function. 

Example 1 :

Find the domain and range of the following function

f(x)  =  x / (1 + x²)

Solution :

Domain of the function f (x) :

f(x)  =  x / (1 + x²)

The denominator will never become zero for any values of x.

Thus f(x) accepts all real values of x.

Hence the domain of the given function is R.

Domain of the function f (x) :

y  =  x / (1 + x²)

y (1 + x²)  = x 

y + yx²  = x

x²y - x + y = 0

Solving for x, we get

x = 1 ± √(1 - 4y²) / 2y

Clearly, x will assume real values if 

1 - 4y² ≥ 0 and y ≠ 0

4y² - 1 ≤ 0 and y ≠ 0

Divide by 4 on both sides

y² - 1/4 ≤ 0

y² - (1/2)² ≤ 0

(y - 1/2) (y + 1/2) ≤ 0 and y ≠ 0

-1/2 ≤ y ≤ 1/2 and y ≠ 0

y ∈ [-1/2, 1/2] - {0}

But, in the original function y = x / (1 + x²), y = 0 for x = 0.

So we have to include "0" in the range.  

Hence, the range of f (x) is [-1/2, 1/2].

Example 2 :

Find the domain and range of the following function

f(x)  =  3 / (2 - x²)

Solution :

Domain of the function f (x) :

f(x)  =  3 / (2 - x²)

To find domain, we need to find out for what values of x the denominator will become zero.

2 - x² = 0

Subtract 2 on both sides

2 - x² - 2  = 0 - 2

- x²   = - 2  ===> x = ± √2

From this, we come to know that the values √2 and -√2 will make the denominator zero.

Hence the domain is R - {± √2}

Range of the function f(x) :

y  =  3 / (2 - x²)

y (2 - x²)  =  3

2y - x² y = 3

2y - 3 = x² y

x²   =  (2y- 3)/y  ==> x = √((2y- 3)/y)

√((2y- 3)/y) ≥ 0

y = 3/2 will make the above term as zero.

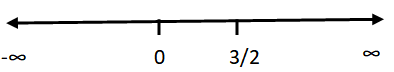
From the above number line, we can split it into three parts.

 (-∞, 0) , (0, 3/2], [3/2, ∞) 

Now we need to apply the values from each intervals. The intervals which satisfies the above condition will be the range.

The values from the intervals  (-∞, 0), [3/2, ∞) satisfies the above condition.

So, the range of f(x) is 

(-∞, 0) U [3/2, ∞)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.