HOW TO FIND THE CENTER AND RADIUS OF A CIRCLE FROM ITS EQUATION

Find the center and radius of the following circles.

Example 1 :

x² + y² = 25

Solution :

The given equation of the circle is in the form of

x² + y² = r²

So, the center of the given circle is (0, 0).

Radius :.

r² = 25

r = 5 units

Example 2 :

(x - 1)² + (y - 3)² = 9

Solution :

The given equation of the circle is in the form of

(x - h)² + (y - k)² = r²

Center :

(h, k) = (0, 0)

Radius :.

r² = 9

r = 3 units

Example 3 :

(x + 3)² + (y - 5)² = 15

Solution :

The given equation of the circle is in the form of

(x - h)² + (y - k)² = r²

Center :

(h, k) = (-3, 5)

Radius :.

r² = 15

r = √15 units

Example 4 :

x² + y²  - 4x  - 6y + 9 = 0

Solution :

The given equation of circle is in general form.

Comparing 

x² + y² - 4x - 6y + 9 = 0

and 

x² + y² + 2gx + 2fy + c = 0

we get

2g = -4 ----> g = -2 ----> -g = 2

2f = -6 ----> f = -3 ----> -f = 3

Center :

(-g, -f) = (2, 3)

Radius :

r = √(g² + f² - c)

= √(4 + 9 - 9)

= √4

= 2 units

Example 5 :

Find the center of the circle described on the line joining the points (1, 2) and (2, 4) as its diameter.

Solution :

Center of the circle = Midpoint of the diameter

Substitute (x₁, y₁) = (1, 2) and (x₂, y₂) = (2, 4).

(1 + 2)/2, (2 + 4)/2

= 3/2, 6/2

= (1.5, 3) is the center of the circle.

Example 6 :

The equation of a circle C, with center O is 

(x - 3)² + (y + 2)² = 25

a) Find the coordinates of the center O.

b)  Find the radius of C.

c)  Show that the point (6, 2) lies on C.

Solution :

(x - 3)² + (y + 2)² = 25

a)

By comparing this equation with 

(x - h)² + (y - k)² = r²

(x - 3)² + (y - (-2))² = 5²

center is (h, k) ==> (3, -2)

b)  radius = 5

c) Applying the point (6, 2) in the equation of circle, we get

(6 - 3)² + (2 + 2)² = 25

3² + 4² = 25

9 + 16 = 25

25 = 25

So, the point (6, 2) lies in the circle.

Example 7 :

A circle has center (5, 2) and radius 4.

(a) Write down the equation of the circle.

(b) Does the point (7, 4) lie on the circle?

Solution :

Center (5, 2) and radius = 4

Equation of circle :

(x - h)² + (y - k)² = r²

(x - 5)² + (y - 2)² = 4²

x² - 10x + 25 + y² - 4y + 4 = 16

x² + y² - 10x - 4y + 4 - 16 = 0

x² + y² - 10x - 4y - 12 = 0

Example 8 :

Find the equation of the circle

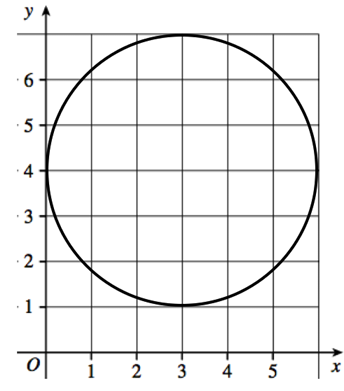
Solution :

From the circle shown, center of the circle is (3, 4)

Distance between (0, 4) and (3, 4)

= √(x₂ - x₁)² + (y₂ - y₁)²

= √(4 - 4)² + (3 - 0)²

= √0² + 3²

= 3

Radius of the circle = 3 units.

Equation of circle :

(x - h)² + (y - k)² = r²

(x - 3)² + (y - 4)² = 3²

x² - 6x + 9 + y² - 8y + 16 = 9

x² + y² - 6x - 8y + 16 - 9 = 0

x² + y² - 6x - 8y + 7 = 0

Example 9 :

A circle C has centre O The points A (0, 6) and B (8, 6) lie on the diameter of C.

(a) Find the coordinates of the centre O.

(b) Write down the equation of the circle.

Solution :

Endpoints of the diameter are A (0, 6) and B (8, 6)

a)

Midpoint of diameter = center of the circle

= (x₁ + x₂)/2, (y₁ + y₂)/2

= (0 + 8)/2, (6 + 6)/2

= 8/2, 12/2

Center of the circle = O (4, 6) 

Distance between center and one endpoint of the diameter 

= √(x₂ - x₁)² + (y₂ - y₁)²

O (4, 6)  and A (0, 6)

= √(x₂ - x₁)² + (y₂ - y₁)²

= √(4 - 0)² + (6 - 6)²

= √4² + 0²

radius = 4

b)

Equation of circle :

(x - 4)² + (y - 6)² = 4²

x² - 8x + 16 + y² - 12y + 36 - 16 = 0

x² + y² - 8x - 12y  + 16 + 36 - 16 = 0

x² + y² - 8x - 12y + 36 = 0

Example 10 :

AB is a diameter of a circle C. O is the centre of the circle A has coordinates (-2, 12) and B has coordinates (8, 2).

(a) Find the centre of the circle, O.

(b) Find the equation of C

(c) Show the point D, (10, 8) lies on C.

Solution :

a) Midpoint of diameter = center of the circle

= (x₁ + x₂)/2, (y₁ + y₂)/2

A(-2, 12) and B(8, 2)

= (-2 + 8)/2, (12 + 2)/2

= 6/2, 14/2

Center = O (3, 7)

Distance between center and one endpoint of the diameter 

= √(x₂ - x₁)² + (y₂ - y₁)²

O (3, 7)  and A (-2, 12)

= √(x₂ - x₁)² + (y₂ - y₁)²

= √(-2 - 3)² + (12 - 7)²

= √(-5)² + 5²

= √(25 + 25)

= √50

Radius = 5√2

b)

Equation of circle :

(x - 3)² + (y - 7)² = √50²

x² - 6x + 9 + y² - 14y + 49 = 50

x² + y² - 6x - 14y + 58 - 50 = 0

x² + y² - 6x - 14y + 8 = 0

c) (x - 3)² + (y - 7)² = √50²

Applying (10, 8), we get

 (10 - 3)² + (8 - 7)² = √50²

7² + 1² = 50

49 + 1 = 50

50 = 50

So, the point lies on the circle.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.