HOW TO FIND THE POINT OF INTERSECTION OF TWO LINES WITHOUT GRAPHING

How to Find Point of Intersection of Two Lines without Graphing ?

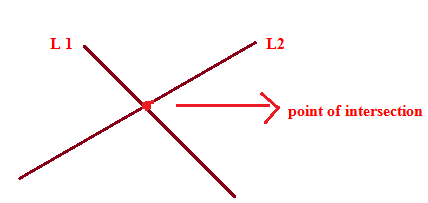
In this page we are going to see how to find the point of intersection of two lines.If two straight lines are not parallel then they will meet at a point. This common point for both straight lines is called the point of intersection.

If the equations of two intersecting straight lines are given,then their intersecting point is obtained by solving equations simultaneously.

Examples of Finding the Points of Intersection

Example 1 :

Find the intersection point of the straight lines

2x - 3y  =  6 and x + y  =  3

Solution :

2x - 3y  =  6    -----(1)

(2) ⋅ 3 ==>3x + 3y = 9

2x - 3y  =  6  

3x + 3y  =  9

------------

5x  =  15

x  =  15/5

x  =  3

By applying x = 3 in (1), we get

2(3) - 3y  =  6

6 - 3y  =  6 

-3y  =  0

y  =  0

So the point of intersection of the given straight lines is (3, 0).

Example 2 :

Find the intersection point of the straight lines

3x + 5y  =  6 and 5x - y  =  10

Solution :

Now we need to solve both the equation.

3x + 5y  =  6    -----(1)

5x - y  =  10     -----(2)

  (2) ⋅ 5 ==> 25x - 5y = 50

3x + 5y  =  6

25x - 5y  =  50 

-------------------

28x  =  56

x  =  2

by applying x  =  2 in (1), we get

3(2) + 5y  =  6

6 + 5y  =  6 

5y  =  6 - 6

5y  =  0

y  =  0

So the answer is  (2, 0).

After having gone through the stuff given above, we hope that the students would have understood how to find the point of intersection of two lines.

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.